Bayesian Longitudinal Multilevel Models

Using brms / STAN

Author

Andy Grogan-Kaylor

Published

August 9, 2024

1 Set Up 🌲

You will need to install the relevant packages: lme4 for frequentist MLM, and brms, which also installs STAN, for Bayesian MLM.

install.packages(c("lme4", "brms"))

2 Gutten Tree Data 🌲

Norway Spruce and Larch Forest in Austrian Alps, https://ec.europa.eu/jrc/en/research-topic/forestry/qr-tree-project/norway-spruce

The data used in this example are derived from the R package Functions and Datasets for “Forest Analytics with R”.

According to the documentation, the source of these data are: “von Guttenberg’s Norway spruce (Picea abies [L.] Karst) tree measurement data.”

The documentation goes on to further note that:

“The data are measures from 107 trees. The trees were selected as being of average size from healthy and well stocked stands in the Alps.”

3 Import The Data 🌲

library(haven)

gutten <- read_dta("gutten.dta")

gutten

# A tibble: 1,200 × 9
   site      location   tree age_base height dbh_cm volume age_bh tree_ID  
   <dbl+lbl> <dbl+lbl> <dbl>    <dbl>  <dbl>  <dbl>  <dbl>  <dbl> <dbl+lbl>
 1 1 [1]     1 [1]         1       20    4.2    4.6      5   9.67 1 [1.1]  
 2 1 [1]     1 [1]         1       30    9.3   10.2     38  19.7  1 [1.1]  
 3 1 [1]     1 [1]         1       40   14.9   14.9    123  29.7  1 [1.1]  
 4 1 [1]     1 [1]         1       50   19.7   18.3    263  39.7  1 [1.1]  
 5 1 [1]     1 [1]         1       60   23     20.7    400  49.7  1 [1.1]  
 6 1 [1]     1 [1]         1       70   25.8   22.6    555  59.7  1 [1.1]  
 7 1 [1]     1 [1]         1       80   27.4   24.1    688  69.7  1 [1.1]  
 8 1 [1]     1 [1]         1       90   28.8   25.5    820  79.7  1 [1.1]  
 9 1 [1]     1 [1]         1      100   30     26.5    928  89.7  1 [1.1]  
10 1 [1]     1 [1]         1      110   30.9   27.3   1023  99.7  1 [1.1]  
# ℹ 1,190 more rows

4 Variables 🌲

site Growth quality class of the tree’s habitat. 5 levels.

location Distinguishes tree location. 7 levels.

tree An identifier for the tree within location.

age.base The tree age taken at ground level.

height Tree height, m.

dbh.cm Tree diameter, cm.

volume Tree volume.

age.bh Tree age taken at 1.3 m.

tree.ID A factor uniquely identifying the tree.

5 A Basic Multilevel Model 🌲

\[\text{height}_{it} = \beta_0 + \beta \text{agebase} + \beta \text{site} + \beta \text{agebase} \times \text{site} + u_{0 \text{ tree.ID}} + e_{it}\]

Both lmer (frequentist MLM) and brms (Bayesian MLM) use the idea of translating the above equation into a formula:

height ~ age_base + site + (1 | tree_ID)

6 Graph (Spaghetti Plot)

Let’s first graph the model to get a visual idea of likely model results.

Code

library(ggplot2)

ggplot(gutten,
       aes(x = age_base, # x is tree age
           y = height)) + # y is tree height
  geom_smooth(aes(color = as.factor(tree_ID)), 
              method = "lm",
              se = FALSE) + # linear model for each tree
  geom_smooth(method = "lm", 
              color = "red",
              size = 2) + # linear model 
  labs(title = "Tree Height As A Function Of Age") +
  scale_color_viridis_d() + # nice graph colors for trees
  theme_minimal() +
  theme(legend.position = "none")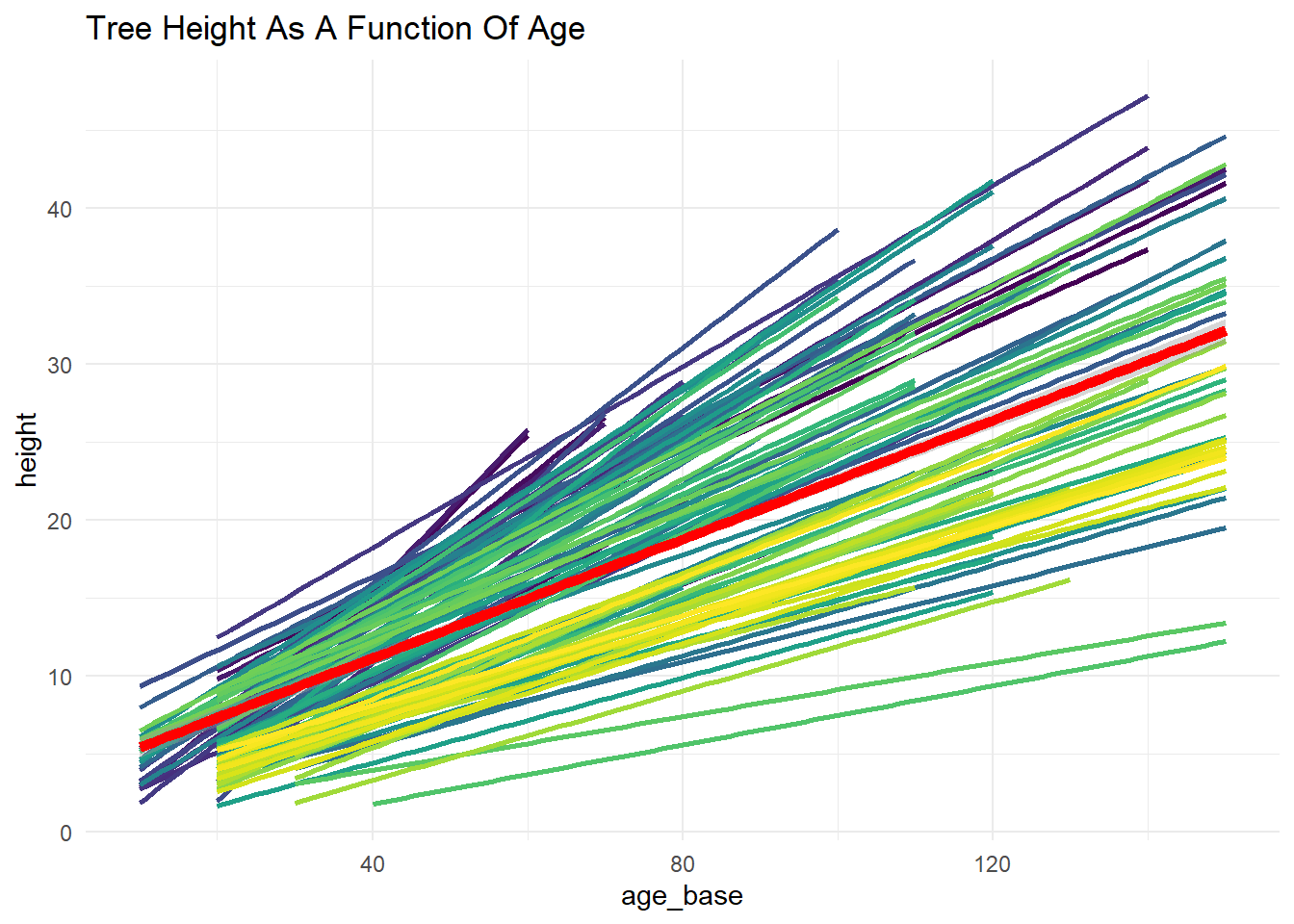

7 Frequentist Model in `lmer` 🌲

NB: * provides both an interaction term and main effects.

library(lme4)

fit1 <- lmer(height ~ age_base * site + (1 | tree_ID), 
             data = gutten)

tab_model(fit1)

	height
Predictors	Estimates	CI	p
(Intercept)	4.74	3.76 – 5.71	<0.001
age.base	0.32	0.32 – 0.33	<0.001
site	-1.01	-1.36 – -0.67	<0.001
age_base:site	-0.04	-0.04 – -0.04	<0.001
Random Effects
σ²	5.04
τ₀₀ _{tree_ID}	2.46
ICC	0.33
N _{tree_ID}	107
Observations	1200
Marginal R² / Conditional R²	0.916 / 0.944

8 Bayesian Model With `brms` (Less Informative Default Priors) 🌲

The models below take a non-trivial amount of time to run.

library(brms)

fit2 <- brm(height ~ age_base * site + (1 | tree_ID), 
            data = gutten,
            family = gaussian(), 
            warmup = 2000, 
            iter = 5000)


SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 0.000283 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 2.83 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 5000 [  0%]  (Warmup)
Chain 1: Iteration:  500 / 5000 [ 10%]  (Warmup)
Chain 1: Iteration: 1000 / 5000 [ 20%]  (Warmup)
Chain 1: Iteration: 1500 / 5000 [ 30%]  (Warmup)
Chain 1: Iteration: 2000 / 5000 [ 40%]  (Warmup)
Chain 1: Iteration: 2001 / 5000 [ 40%]  (Sampling)
Chain 1: Iteration: 2500 / 5000 [ 50%]  (Sampling)
Chain 1: Iteration: 3000 / 5000 [ 60%]  (Sampling)
Chain 1: Iteration: 3500 / 5000 [ 70%]  (Sampling)
Chain 1: Iteration: 4000 / 5000 [ 80%]  (Sampling)
Chain 1: Iteration: 4500 / 5000 [ 90%]  (Sampling)
Chain 1: Iteration: 5000 / 5000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 12.315 seconds (Warm-up)
Chain 1:                7.296 seconds (Sampling)
Chain 1:                19.611 seconds (Total)
Chain 1: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
Chain 2: 
Chain 2: Gradient evaluation took 7.8e-05 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.78 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2: 
Chain 2: 
Chain 2: Iteration:    1 / 5000 [  0%]  (Warmup)
Chain 2: Iteration:  500 / 5000 [ 10%]  (Warmup)
Chain 2: Iteration: 1000 / 5000 [ 20%]  (Warmup)
Chain 2: Iteration: 1500 / 5000 [ 30%]  (Warmup)
Chain 2: Iteration: 2000 / 5000 [ 40%]  (Warmup)
Chain 2: Iteration: 2001 / 5000 [ 40%]  (Sampling)
Chain 2: Iteration: 2500 / 5000 [ 50%]  (Sampling)
Chain 2: Iteration: 3000 / 5000 [ 60%]  (Sampling)
Chain 2: Iteration: 3500 / 5000 [ 70%]  (Sampling)
Chain 2: Iteration: 4000 / 5000 [ 80%]  (Sampling)
Chain 2: Iteration: 4500 / 5000 [ 90%]  (Sampling)
Chain 2: Iteration: 5000 / 5000 [100%]  (Sampling)
Chain 2: 
Chain 2:  Elapsed Time: 11.462 seconds (Warm-up)
Chain 2:                7.208 seconds (Sampling)
Chain 2:                18.67 seconds (Total)
Chain 2: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 3).
Chain 3: 
Chain 3: Gradient evaluation took 7.3e-05 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.73 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3: 
Chain 3: 
Chain 3: Iteration:    1 / 5000 [  0%]  (Warmup)
Chain 3: Iteration:  500 / 5000 [ 10%]  (Warmup)
Chain 3: Iteration: 1000 / 5000 [ 20%]  (Warmup)
Chain 3: Iteration: 1500 / 5000 [ 30%]  (Warmup)
Chain 3: Iteration: 2000 / 5000 [ 40%]  (Warmup)
Chain 3: Iteration: 2001 / 5000 [ 40%]  (Sampling)
Chain 3: Iteration: 2500 / 5000 [ 50%]  (Sampling)
Chain 3: Iteration: 3000 / 5000 [ 60%]  (Sampling)
Chain 3: Iteration: 3500 / 5000 [ 70%]  (Sampling)
Chain 3: Iteration: 4000 / 5000 [ 80%]  (Sampling)
Chain 3: Iteration: 4500 / 5000 [ 90%]  (Sampling)
Chain 3: Iteration: 5000 / 5000 [100%]  (Sampling)
Chain 3: 
Chain 3:  Elapsed Time: 11.49 seconds (Warm-up)
Chain 3:                7.058 seconds (Sampling)
Chain 3:                18.548 seconds (Total)
Chain 3: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 4).
Chain 4: 
Chain 4: Gradient evaluation took 9e-05 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.9 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4: 
Chain 4: 
Chain 4: Iteration:    1 / 5000 [  0%]  (Warmup)
Chain 4: Iteration:  500 / 5000 [ 10%]  (Warmup)
Chain 4: Iteration: 1000 / 5000 [ 20%]  (Warmup)
Chain 4: Iteration: 1500 / 5000 [ 30%]  (Warmup)
Chain 4: Iteration: 2000 / 5000 [ 40%]  (Warmup)
Chain 4: Iteration: 2001 / 5000 [ 40%]  (Sampling)
Chain 4: Iteration: 2500 / 5000 [ 50%]  (Sampling)
Chain 4: Iteration: 3000 / 5000 [ 60%]  (Sampling)
Chain 4: Iteration: 3500 / 5000 [ 70%]  (Sampling)
Chain 4: Iteration: 4000 / 5000 [ 80%]  (Sampling)
Chain 4: Iteration: 4500 / 5000 [ 90%]  (Sampling)
Chain 4: Iteration: 5000 / 5000 [100%]  (Sampling)
Chain 4: 
Chain 4:  Elapsed Time: 12.537 seconds (Warm-up)
Chain 4:                7.192 seconds (Sampling)
Chain 4:                19.729 seconds (Total)
Chain 4:

tab_model(fit2)

	height
Predictors	Estimates	CI (95%)
Intercept	4.74	3.76 – 5.74
age.base	0.32	0.32 – 0.33
site	-1.01	-1.37 – -0.67
age_base:site	-0.04	-0.04 – -0.04
Random Effects
σ²	5.05
τ₀₀ _{tree_ID}	2.53
ICC	0.33
N _{tree_ID}	107
Observations	1200
Marginal R² / Conditional R²	0.915 / 0.941

9 Set Informative Priors 🌲

prior1 <- c(
  prior(normal(0, 10), class = Intercept), 
  prior(normal(0, 10), class = b, coef = site) #,
  # prior(cauchy(0, 10), class = sigma)
)

10 Run The Model With More Informative Prior 🌲

fit3 <- brm(height ~ age_base * site + (1 | tree_ID), 
            data = gutten,
            family = gaussian(), 
            prior = prior1,
            warmup = 2000, 
            iter = 5000)


SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 0.000275 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 2.75 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 5000 [  0%]  (Warmup)
Chain 1: Iteration:  500 / 5000 [ 10%]  (Warmup)
Chain 1: Iteration: 1000 / 5000 [ 20%]  (Warmup)
Chain 1: Iteration: 1500 / 5000 [ 30%]  (Warmup)
Chain 1: Iteration: 2000 / 5000 [ 40%]  (Warmup)
Chain 1: Iteration: 2001 / 5000 [ 40%]  (Sampling)
Chain 1: Iteration: 2500 / 5000 [ 50%]  (Sampling)
Chain 1: Iteration: 3000 / 5000 [ 60%]  (Sampling)
Chain 1: Iteration: 3500 / 5000 [ 70%]  (Sampling)
Chain 1: Iteration: 4000 / 5000 [ 80%]  (Sampling)
Chain 1: Iteration: 4500 / 5000 [ 90%]  (Sampling)
Chain 1: Iteration: 5000 / 5000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 13.036 seconds (Warm-up)
Chain 1:                6.752 seconds (Sampling)
Chain 1:                19.788 seconds (Total)
Chain 1: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
Chain 2: 
Chain 2: Gradient evaluation took 7.1e-05 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.71 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2: 
Chain 2: 
Chain 2: Iteration:    1 / 5000 [  0%]  (Warmup)
Chain 2: Iteration:  500 / 5000 [ 10%]  (Warmup)
Chain 2: Iteration: 1000 / 5000 [ 20%]  (Warmup)
Chain 2: Iteration: 1500 / 5000 [ 30%]  (Warmup)
Chain 2: Iteration: 2000 / 5000 [ 40%]  (Warmup)
Chain 2: Iteration: 2001 / 5000 [ 40%]  (Sampling)
Chain 2: Iteration: 2500 / 5000 [ 50%]  (Sampling)
Chain 2: Iteration: 3000 / 5000 [ 60%]  (Sampling)
Chain 2: Iteration: 3500 / 5000 [ 70%]  (Sampling)
Chain 2: Iteration: 4000 / 5000 [ 80%]  (Sampling)
Chain 2: Iteration: 4500 / 5000 [ 90%]  (Sampling)
Chain 2: Iteration: 5000 / 5000 [100%]  (Sampling)
Chain 2: 
Chain 2:  Elapsed Time: 12.69 seconds (Warm-up)
Chain 2:                7.334 seconds (Sampling)
Chain 2:                20.024 seconds (Total)
Chain 2: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 3).
Chain 3: 
Chain 3: Gradient evaluation took 0.000161 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 1.61 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3: 
Chain 3: 
Chain 3: Iteration:    1 / 5000 [  0%]  (Warmup)
Chain 3: Iteration:  500 / 5000 [ 10%]  (Warmup)
Chain 3: Iteration: 1000 / 5000 [ 20%]  (Warmup)
Chain 3: Iteration: 1500 / 5000 [ 30%]  (Warmup)
Chain 3: Iteration: 2000 / 5000 [ 40%]  (Warmup)
Chain 3: Iteration: 2001 / 5000 [ 40%]  (Sampling)
Chain 3: Iteration: 2500 / 5000 [ 50%]  (Sampling)
Chain 3: Iteration: 3000 / 5000 [ 60%]  (Sampling)
Chain 3: Iteration: 3500 / 5000 [ 70%]  (Sampling)
Chain 3: Iteration: 4000 / 5000 [ 80%]  (Sampling)
Chain 3: Iteration: 4500 / 5000 [ 90%]  (Sampling)
Chain 3: Iteration: 5000 / 5000 [100%]  (Sampling)
Chain 3: 
Chain 3:  Elapsed Time: 11.387 seconds (Warm-up)
Chain 3:                7.438 seconds (Sampling)
Chain 3:                18.825 seconds (Total)
Chain 3: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 4).
Chain 4: 
Chain 4: Gradient evaluation took 7.2e-05 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.72 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4: 
Chain 4: 
Chain 4: Iteration:    1 / 5000 [  0%]  (Warmup)
Chain 4: Iteration:  500 / 5000 [ 10%]  (Warmup)
Chain 4: Iteration: 1000 / 5000 [ 20%]  (Warmup)
Chain 4: Iteration: 1500 / 5000 [ 30%]  (Warmup)
Chain 4: Iteration: 2000 / 5000 [ 40%]  (Warmup)
Chain 4: Iteration: 2001 / 5000 [ 40%]  (Sampling)
Chain 4: Iteration: 2500 / 5000 [ 50%]  (Sampling)
Chain 4: Iteration: 3000 / 5000 [ 60%]  (Sampling)
Chain 4: Iteration: 3500 / 5000 [ 70%]  (Sampling)
Chain 4: Iteration: 4000 / 5000 [ 80%]  (Sampling)
Chain 4: Iteration: 4500 / 5000 [ 90%]  (Sampling)
Chain 4: Iteration: 5000 / 5000 [100%]  (Sampling)
Chain 4: 
Chain 4:  Elapsed Time: 10.636 seconds (Warm-up)
Chain 4:                6.933 seconds (Sampling)
Chain 4:                17.569 seconds (Total)
Chain 4:

tab_model(fit3)

	height
Predictors	Estimates	CI (95%)
Intercept	4.72	3.72 – 5.73
age.base	0.32	0.32 – 0.33
site	-1.01	-1.37 – -0.66
age_base:site	-0.04	-0.04 – -0.04
Random Effects
σ²	5.05
τ₀₀ _{tree_ID}	2.53
ICC	0.33
N _{tree_ID}	107
Observations	1200
Marginal R² / Conditional R²	0.915 / 0.941

11 Plot Posterior Distributions and Trace Plots 🌲

plot(fit3) will give me a reasonable plot of every parameter, but the layout may not be optimal. I am using separate plot calls below, but to do so, I need to know the names of the parameters, which can be tricky in brms. One way to do this is to use plot(fit3) to see all the parameter names, and then divide the single plot call into multiple plot calls to improve the layout.

# plot(fit3)

plot(fit3, variable = c("b_Intercept"))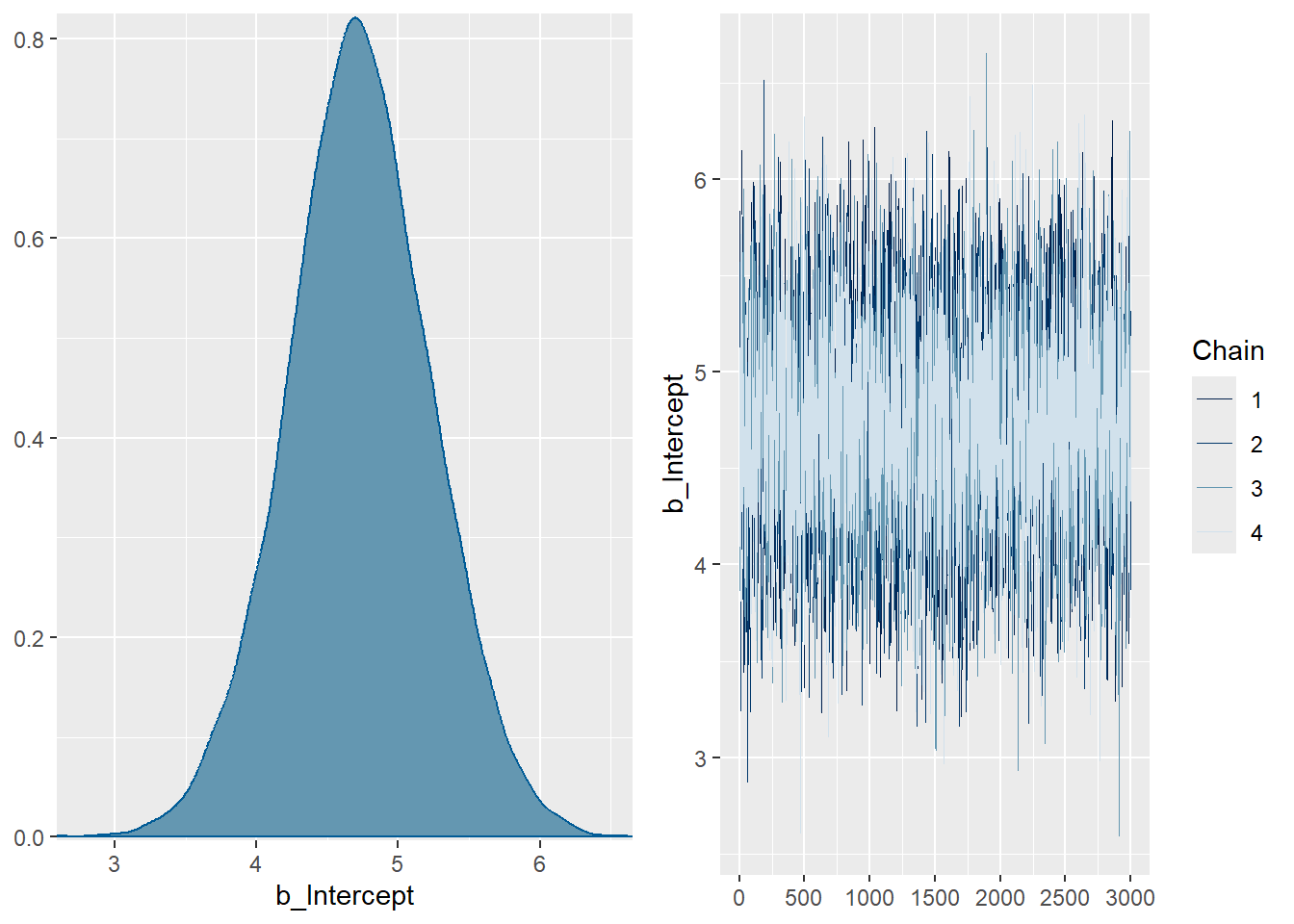

plot(fit3, 
     variable = c("b_age_base", 
                  "b_site",
                  "b_age_base:site")) # regression slopes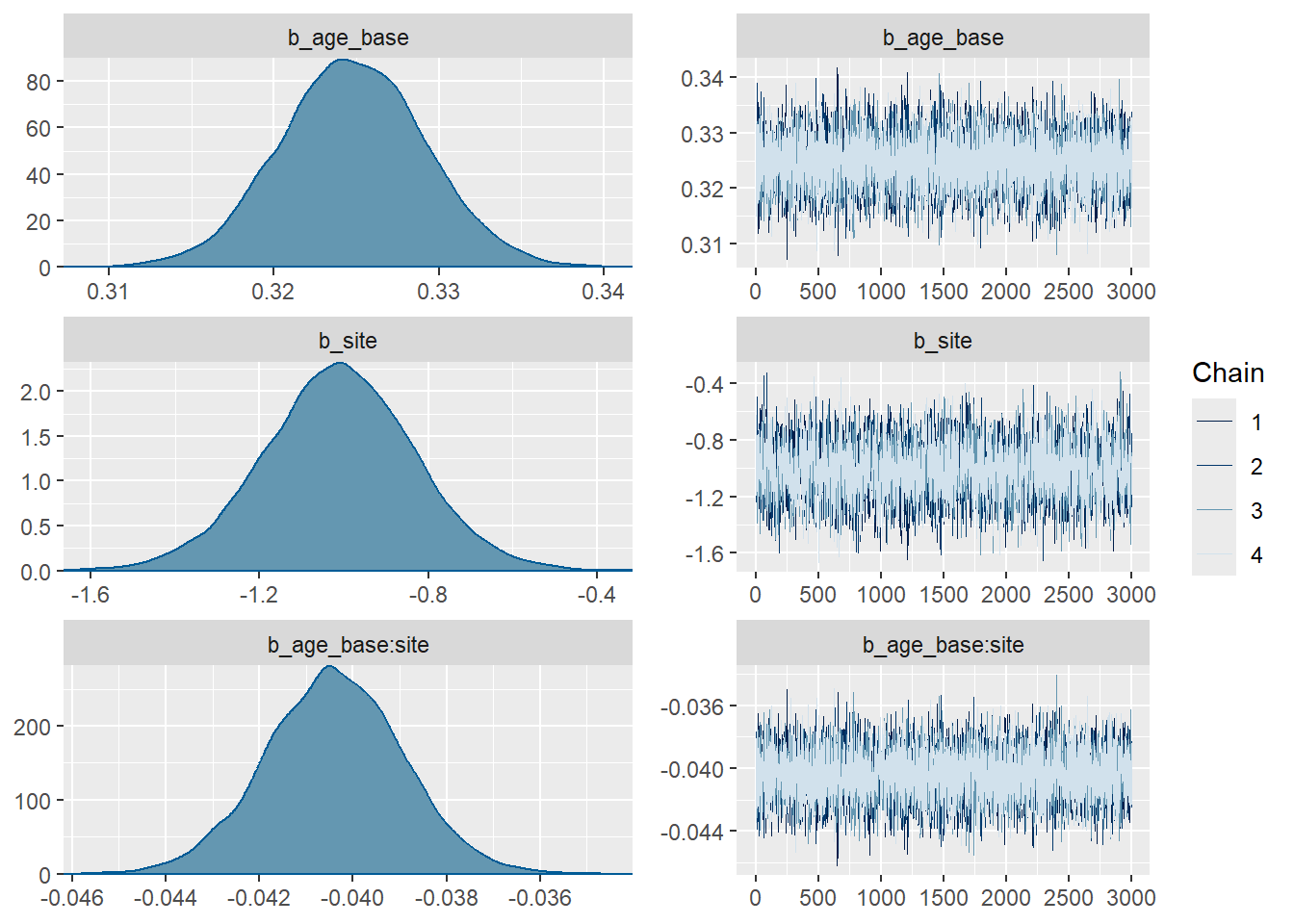

plot(fit3, variable = c("sd_tree_ID__Intercept",
                        "sigma")) # variance parameters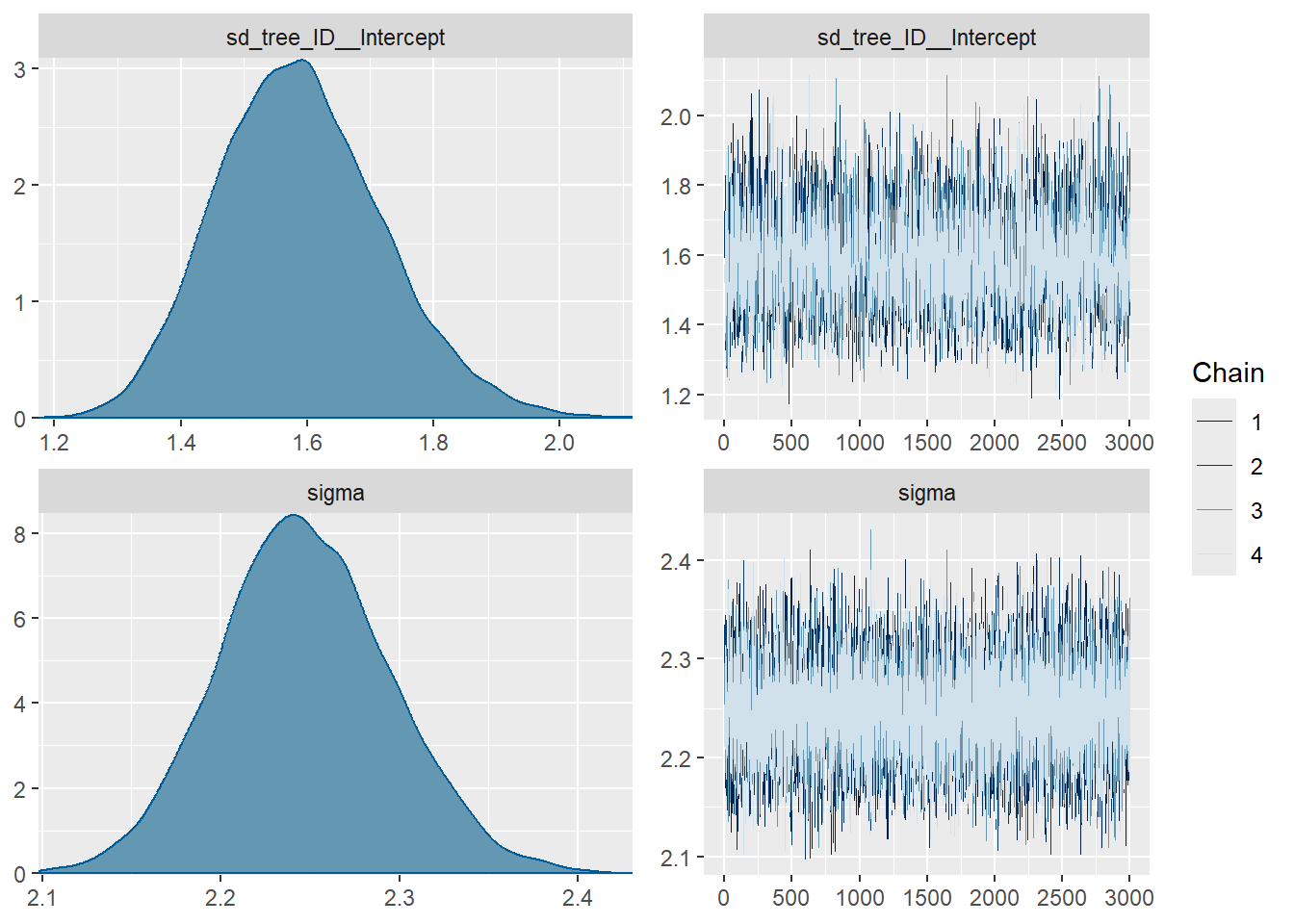

12 Compare All 3 Models 🌲

tab_model(fit1, fit2, fit3,
          dv.labels = c("lmer", "brms default priors", "brms informative priors"), 
          show.se = TRUE,
          show.ci = 0.95,
          show.stat = TRUE)

	lmer					brms default priors			brms informative priors
Predictors	Estimates	std. Error	CI	Statistic	p	Estimates	std. Error	CI (95%)	Estimates	std. Error	CI (95%)
(Intercept)	4.74	0.50	3.76 – 5.71	9.52	<0.001
age.base	0.32	0.00	0.32 – 0.33	72.99	<0.001	0.32	0.00	0.32 – 0.33	0.32	0.00	0.32 – 0.33
site	-1.01	0.18	-1.36 – -0.67	-5.79	<0.001	-1.01	0.18	-1.37 – -0.67	-1.01	0.17	-1.37 – -0.66
age_base:site	-0.04	0.00	-0.04 – -0.04	-27.15	<0.001	-0.04	0.00	-0.04 – -0.04	-0.04	0.00	-0.04 – -0.04
Intercept						4.74	0.51	3.76 – 5.74	4.72	0.49	3.72 – 5.73
Random Effects
σ²	5.04					5.05			5.05
τ₀₀	2.46 _{tree_ID}					2.53 _{tree_ID}			2.53 _{tree_ID}
ICC	0.33					0.33			0.33
N	107 _{tree_ID}					107 _{tree_ID}			107 _{tree_ID}
Observations	1200					1200			1200
Marginal R² / Conditional R²	0.916 / 0.944					0.915 / 0.941			0.915 / 0.941