Contingency Tables
Andy Grogan-Kaylor
Key Concepts and Commands
- Matrices of data
- Probabilities, risks, and odds
- \(\chi^2\) Tests
tabulate x y, row col chi2
Flipping Two Coins
Coin Emoji From Apple
Coin Emoji From Apple
Setup
Good value labels are key here.
. label define nickel ///
> 1 "heads for nickel" ///
> 0 "tails for nickel" // define value label
. label define quarter ///
> 1 "heads for quarter" ///
> 0 "tails for quarter" // define value label
. set obs 1000 // 1000 observations
Number of observations (_N) was 0, now 1,000.
. * curiously it takes around 1000 obs for the proportions
. * below to "take hold"
. generate nickel = rbinomial(1, .75) // unfair nickel
. generate quarter = rbinomial(1, .5) // fair quarter
. label values nickel nickel // assign value label
. label values quarter quarter // assign value label
The Graph We Think We Want But Don’t
. graph bar, over(nickel) scheme(burd) title(Nickel) name(nickel)
. graph bar, over(quarter) scheme(burd) title(Quarter) name(quarter)
. graph combine nickel quarter, title(Nickel And Quarter) scheme(burd)
. graph export unhelpfulgraph.png, width(500) replace
file
/Users/agrogan/Desktop/GitHub/newstuff/categorical/contingency-tables/unhelpfulgraph.p
> ng saved as PNG format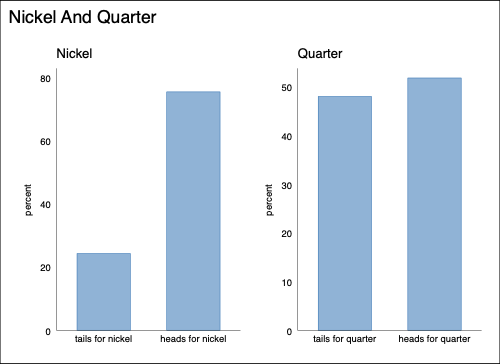
A Graph That May Not Be That Helpful
Crosstabulation
. tabulate nickel quarter, row col
┌───────────────────┐
│ Key │
├───────────────────┤
│ frequency │
│ row percentage │
│ column percentage │
└───────────────────┘
│ quarter
nickel │ tails for heads for │ Total
─────────────────┼──────────────────────┼──────────
tails for nickel │ 104 140 │ 244
│ 42.62 57.38 │ 100.00
│ 21.62 26.97 │ 24.40
─────────────────┼──────────────────────┼──────────
heads for nickel │ 377 379 │ 756
│ 49.87 50.13 │ 100.00
│ 78.38 73.03 │ 75.60
─────────────────┼──────────────────────┼──────────
Total │ 481 519 │ 1,000
│ 48.10 51.90 │ 100.00
│ 100.00 100.00 │ 100.00
Graphing (Mosaic Plot)
. * ssc install spineplot // mosaicplots (spineplots)
. * ssc install scheme-burd, replace // BuRd graph scheme
. spineplot nickel quarter, scheme(burd)
. graph export nickel-quarter.png, width(500) replace
file
/Users/agrogan/Desktop/GitHub/newstuff/categorical/contingency-tables/nickel-quarter.p
> ng saved as PNG format
Mosaic Plot
Bar Chart
Does a bar chart work to visualize these relationships?
. graph bar, over(quarter) over(nickel) scheme(burd)
. graph export nickel-quarter-bar1.png, width(500) replace
file
/Users/agrogan/Desktop/GitHub/newstuff/categorical/contingency-tables/nickel-quarter-b
> ar1.png saved as PNG format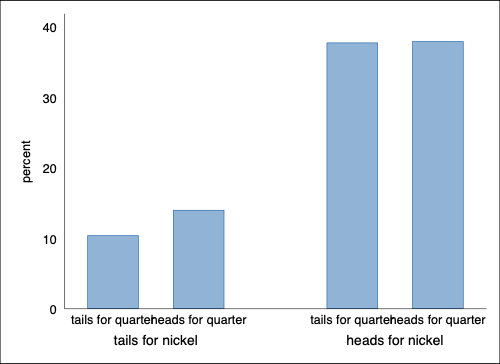
Bar Chart 1
Bar Chart (2)
Option asyvars adds a crucial color element.
. graph bar, over(quarter) over(nickel) scheme(burd) asyvars
. graph export nickel-quarter-bar2.png, width(500) replace
file
/Users/agrogan/Desktop/GitHub/newstuff/categorical/contingency-tables/nickel-quarter-b
> ar2.png saved as PNG format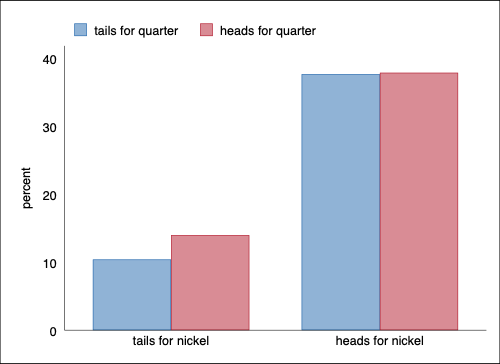
Bar Chart 2
Horizontal Bar Chart
And hbar may improve legibility even more.
. graph hbar, over(quarter) over(nickel) scheme(burd) asyvars
. graph export nickel-quarter-bar3.png, width(500) replace
file
/Users/agrogan/Desktop/GitHub/newstuff/categorical/contingency-tables/nickel-quarter-b
> ar3.png saved as PNG format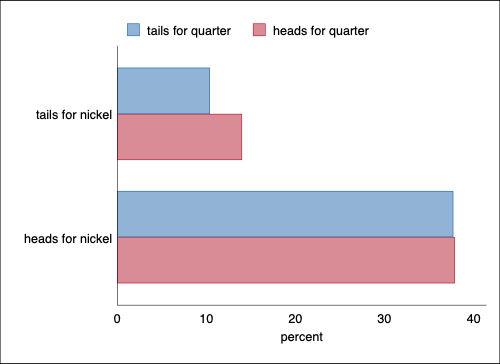
Bar Chart 3
Define Matrix
. matrix input FrenchSkiiers = (31, 109 \ 17, 122)
. matrix rownames FrenchSkiiers = Placebo AscorbicAcid
. matrix colnames FrenchSkiiers = Cold NoCold
. matrix list FrenchSkiiers
FrenchSkiiers[2,2]
Cold NoCold
Placebo 31 109
AscorbicAcid 17 122
Try Making a Data Set From Matrix
. svmat FrenchSkiiers, name(count)
number of observations will be reset to 2
Press any key to continue, or Break to abort
Number of observations (_N) was 0, now 2.
. list
┌─────────────────┐
│ count1 count2 │
├─────────────────┤
1. │ 31 109 │
2. │ 17 122 │
└─────────────────┘
Enter Data By Hand
There are many alternative commands to do this, but the easiest way
is using edit.
I have already done this. Note the structure of the data is different
from above.
. use "FrenchSkiiers.dta", clear
. list // list the data
┌─────────────────────────────────┐
│ Tx Outcome Count │
├─────────────────────────────────┤
1. │ Ascorbic Acid Cold 17 │
2. │ Ascorbic Acid No Cold 122 │
3. │ Placebo Cold 31 │
4. │ Placebo No Cold 109 │
└─────────────────────────────────┘
Mosaic Plot
. spineplot Tx Outcome, scheme(burd)
. graph export FrenchSkiiers1.png, width(500) replace
file
/Users/agrogan/Desktop/GitHub/newstuff/categorical/contingency-tables/FrenchSkiiers1.p
> ng saved as PNG format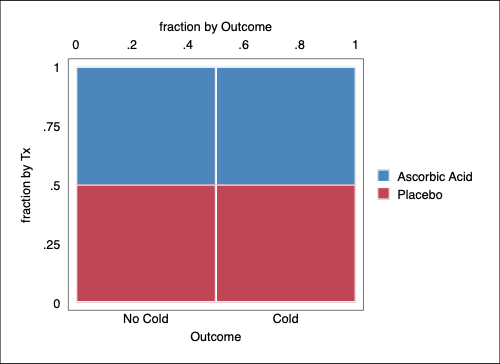
Mosaic Plot Attempt 1
Mosaic Plot (2)
. spineplot Outcome Tx [fweight=Count], scheme(burd) // order matters to interpretability
. graph export FrenchSkiiers2.png, width(500) replace
file
/Users/agrogan/Desktop/GitHub/newstuff/categorical/contingency-tables/FrenchSkiiers2.p
> ng saved as PNG format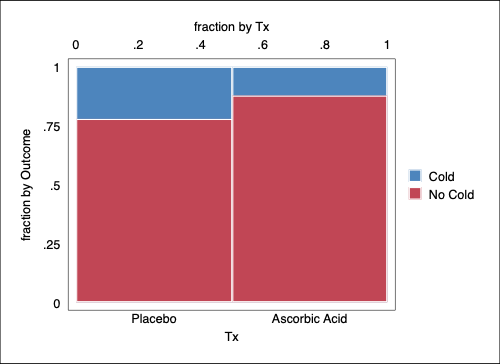
Mosaic Plot Attempt 2
Definitions and Notation
Counts
\(\begin{matrix} c_{ij} & c_{ij} &
c_{i\bullet} \\ c_{ij} & c_{ij} & c_{i\bullet} \\ c_{\bullet j}
& c_{\bullet j} & c_{\bullet \bullet} \\
\end{matrix}\)
Probabilities
\(\begin{matrix}p_{ij} & p_{ij} &
p_{i\bullet} \\ p_{ij} & p_{ij} & p_{i \bullet} \\ p_{\bullet j}
& p_{\bullet j} & p_{\bullet \bullet} \\
\end{matrix}\)
Terms
\(p_{ij}\) are joint
probabilities.
\(p_{i \bullet}\) and \(p_{\bullet j}\) are marginal
probabilities.
\(p_{ij} \mid p_{i \bullet}\) and
\(p_{ij} \mid p_{\bullet j}\) are
conditional probabilities.
Fundamental Rule
\[\text{conditional = joint /
marginal}\]
. tabulate Tx Outcome [fweight = Count], cell row col
┌───────────────────┐
│ Key │
├───────────────────┤
│ frequency │
│ row percentage │
│ column percentage │
│ cell percentage │
└───────────────────┘
│ Outcome
Tx │ No Cold Cold │ Total
──────────────┼──────────────────────┼──────────
Placebo │ 109 31 │ 140
│ 77.86 22.14 │ 100.00
│ 47.19 64.58 │ 50.18
│ 39.07 11.11 │ 50.18
──────────────┼──────────────────────┼──────────
Ascorbic Acid │ 122 17 │ 139
│ 87.77 12.23 │ 100.00
│ 52.81 35.42 │ 49.82
│ 43.73 6.09 │ 49.82
──────────────┼──────────────────────┼──────────
Total │ 231 48 │ 279
│ 82.80 17.20 │ 100.00
│ 100.00 100.00 │ 100.00
│ 82.80 17.20 │ 100.00
. display 6.09 / 49.82
.12224006
. display 17/139
.12230216
Independence (Robert Mare)
If independence is true, then joint probabilities = products of
marginal probabilities.
That is, under independence, the conditional distribution equals the
marginal distribution.
Under independence, row membership provides no information about the
column distribution; and column membership provides no information about
the row distribution.
Independence is a model, which is never exactly true in the real
world.
Observed vs. Expected
. tabulate Tx Outcome [fweight = Count]
│ Outcome
Tx │ No Cold Cold │ Total
──────────────┼──────────────────────┼──────────
Placebo │ 109 31 │ 140
Ascorbic Acid │ 122 17 │ 139
──────────────┼──────────────────────┼──────────
Total │ 231 48 │ 279
. scalar N = 31 + 109 + 17 + 122
. scalar A = ((31 + 17)*(31 + 109)) / N // expected count
. scalar B = ((31 + 109)*(109 + 122)) / N // expected count
. scalar C = ((31 + 17) * (17 + 122)) / N // expected count
. scalar D = ((17 + 122) * (109 + 122)) / N // expected count
. matrix FS = (A, B \ C, D) // matrix of expected values
. matrix rownames FS = Placebo AscorbicAcid // rownames
. matrix colnames FS = Cold NoCold // column names
. matrix list FS
FS[2,2]
Cold NoCold
Placebo 24.086022 115.91398
AscorbicAcid 23.913978 115.08602
Chi-Square Test
\(\chi^2 = \Sigma
\frac{(O-E)^2}{E}\)
. scalar chisquare = (31 - 24.086022)^2 / 24.086022 + ///
> (109 - 115.91398)^2 / 115.91398 + ///
> (17 - 23.913978)^2 / 23.913978 + ///
> (122 - 115.08602)^2 / 115.08602
. scalar list chisquare
chisquare = 4.8114124
Compare With Tabulate
. use "FrenchSkiiers.dta", clear
. tabulate Tx Outcome [fweight = Count], row col chi2
┌───────────────────┐
│ Key │
├───────────────────┤
│ frequency │
│ row percentage │
│ column percentage │
└───────────────────┘
│ Outcome
Tx │ No Cold Cold │ Total
──────────────┼──────────────────────┼──────────
Placebo │ 109 31 │ 140
│ 77.86 22.14 │ 100.00
│ 47.19 64.58 │ 50.18
──────────────┼──────────────────────┼──────────
Ascorbic Acid │ 122 17 │ 139
│ 87.77 12.23 │ 100.00
│ 52.81 35.42 │ 49.82
──────────────┼──────────────────────┼──────────
Total │ 231 48 │ 279
│ 82.80 17.20 │ 100.00
│ 100.00 100.00 │ 100.00
Pearson chi2(1) = 4.8114 Pr = 0.028
Risk Differences and Risk Ratios (Relative Risk)
Following Viera, 2008:
\(\begin{bmatrix}a & b \\ c &
d\end{bmatrix}\)
| Exposed |
a |
b |
| Not Exposed |
c |
d |
\(R = \frac{a}{a+b}\) (in
Exposed)
\(RR =\frac{\text{risk in
exposed}}{\text{risk in not exposed}} =
\frac{a/(a+b)}{c/(c+d)}\)
Calculating a Risk Ratio
. tabulate Outcome Tx [fweight = Count]
│ Tx
Outcome │ Placebo Ascorbic │ Total
───────────┼──────────────────────┼──────────
No Cold │ 109 122 │ 231
Cold │ 31 17 │ 48
───────────┼──────────────────────┼──────────
Total │ 140 139 │ 279
. tabulate Outcome Tx [fweight = Count], col
┌───────────────────┐
│ Key │
├───────────────────┤
│ frequency │
│ column percentage │
└───────────────────┘
│ Tx
Outcome │ Placebo Ascorbic │ Total
───────────┼──────────────────────┼──────────
No Cold │ 109 122 │ 231
│ 77.86 87.77 │ 82.80
───────────┼──────────────────────┼──────────
Cold │ 31 17 │ 48
│ 22.14 12.23 │ 17.20
───────────┼──────────────────────┼──────────
Total │ 140 139 │ 279
│ 100.00 100.00 │ 100.00
. display 31/140
.22142857
. display 17/139
.12230216
. display (17/139) / (31/140)
.55233233
. csi 17 31 122 109 // also has an intuitive dialog box
│ Exposed Unexposed │ Total
─────────────────┼────────────────────────┼───────────
Cases │ 17 31 │ 48
Noncases │ 122 109 │ 231
─────────────────┼────────────────────────┼───────────
Total │ 139 140 │ 279
│ │
Risk │ .1223022 .2214286 │ .172043
│ │
│ Point estimate │ [95% conf. interval]
├────────────────────────┼────────────────────────
Risk difference │ -.0991264 │ -.1868592 -.0113937
Risk ratio │ .5523323 │ .3209178 .9506203
Prev. frac. ex. │ .4476677 │ .0493797 .6790822
Prev. frac. pop │ .2230316 │
└────────────────────────┴────────────────────────
chi2(1) = 4.81 Pr>chi2 = 0.0283
Odds Ratios
| Exposed |
a |
b |
| Not Exposed |
c |
d |
\(OR =\)
\(\frac{\text{odds that exposed person
develops outcome}}{\text{odds that unexposed person develops
outcome}}\)
\(= \frac{\frac{a}{a+b} /
\frac{b}{a+b}}{\frac{c}{c+d} / \frac{d}{c+d}} = \frac{a/b}{c/d} =
\frac{ad}{bc}\)
Properties of the Odds Ratio (Robert Mare)
In general for the 2 X 2 Table,
\(0 < OR < 1\)
indicates that one row is less likely to make the first response than
the other row.
\(1 < OR < \infty\)
indicates that one row is more likely to make the first response than
the other row.
Calculate Odds Ratio
. tabulate Tx Outcome [fweight = Count]
│ Outcome
Tx │ No Cold Cold │ Total
──────────────┼──────────────────────┼──────────
Placebo │ 109 31 │ 140
Ascorbic Acid │ 122 17 │ 139
──────────────┼──────────────────────┼──────────
Total │ 231 48 │ 279
. display (17 * 109)/(122 * 31)
.48995241
. csi 17 31 122 109, or // also has an intuitive dialog box
│ Exposed Unexposed │ Total
─────────────────┼────────────────────────┼───────────
Cases │ 17 31 │ 48
Noncases │ 122 109 │ 231
─────────────────┼────────────────────────┼───────────
Total │ 139 140 │ 279
│ │
Risk │ .1223022 .2214286 │ .172043
│ │
│ Point estimate │ [95% conf. interval]
├────────────────────────┼────────────────────────
Risk difference │ -.0991264 │ -.1868592 -.0113937
Risk ratio │ .5523323 │ .3209178 .9506203
Prev. frac. ex. │ .4476677 │ .0493797 .6790822
Prev. frac. pop │ .2230316 │
Odds ratio │ .4899524 │ .2588072 .9282861 (Cornfield)
└────────────────────────┴────────────────────────
chi2(1) = 4.81 Pr>chi2 = 0.0283