30 Jun 2021 09:14:56
DRAFT VERSION: COMMENTS, QUESTIONS AND CORRECTIONS WELCOME.
In another handout, we have discussed the idea that interactions in logistic regression models require careful interpretation. In this handout, we discuss the idea that, because logistic regression models are inherently non-linear–marginal change depends upon the value of the x’s–logistic regression models may have an interactive quality, even when no interaction is directly specified.
. use http://www.stata-press.com/data/r15/margex, clear // simulated data for margins (Artificial data for margins)
. regress outcome age i.group // linear model with only main effects, no interactions
Source │ SS df MS Number of obs = 3,000
─────────────┼────────────────────────────────── F(3, 2996) = 208.92
Model │ 73.1197372 3 24.3732457 Prob > F = 0.0000
Residual │ 349.519929 2,996 .116662193 R-squared = 0.1730
─────────────┼────────────────────────────────── Adj R-squared = 0.1722
Total │ 422.639667 2,999 .140926865 Root MSE = .34156
─────────────┬────────────────────────────────────────────────────────────────
outcome │ Coefficient Std. err. t P>|t| [95% conf. interval]
─────────────┼────────────────────────────────────────────────────────────────
age │ .0099798 .000643 15.52 0.000 .0087191 .0112405
│
group │
2 │ -.1244143 .0152899 -8.14 0.000 -.1543941 -.0944345
3 │ -.1325247 .0193249 -6.86 0.000 -.1704162 -.0946332
│
_cons │ -.1509829 .0316164 -4.78 0.000 -.2129749 -.0889909
─────────────┴────────────────────────────────────────────────────────────────
. margins group, at(age = (20(10)60)) // calculate margins
Adjusted predictions Number of obs = 3,000
Model VCE: OLS
Expression: Linear prediction, predict()
1._at: age = 20
2._at: age = 30
3._at: age = 40
4._at: age = 50
5._at: age = 60
─────────────┬────────────────────────────────────────────────────────────────
│ Delta-method
│ Margin std. err. t P>|t| [95% conf. interval]
─────────────┼────────────────────────────────────────────────────────────────
_at#group │
1 1 │ .0486131 .0198096 2.45 0.014 .0097713 .0874549
1 2 │ -.0758012 .0153896 -4.93 0.000 -.1059765 -.0456258
1 3 │ -.0839116 .0147861 -5.68 0.000 -.1129036 -.0549196
2 1 │ .1484111 .0145895 10.17 0.000 .1198048 .1770175
2 2 │ .0239968 .011409 2.10 0.036 .0016266 .0463671
2 3 │ .0158864 .0130784 1.21 0.225 -.0097571 .04153
3 1 │ .2482091 .0107686 23.05 0.000 .2270946 .2693236
3 2 │ .1237948 .0103038 12.01 0.000 .1035917 .143998
3 3 │ .1156844 .0143575 8.06 0.000 .0875329 .1438359
4 1 │ .3480071 .0100871 34.50 0.000 .3282287 .3677855
4 2 │ .2235928 .0128393 17.41 0.000 .198418 .2487677
4 3 │ .2154824 .0179975 11.97 0.000 .1801938 .2507711
5 1 │ .4478051 .0130467 34.32 0.000 .4222237 .4733865
5 2 │ .3233908 .0174988 18.48 0.000 .2890799 .3577017
5 3 │ .3152804 .0228989 13.77 0.000 .2703813 .3601795
─────────────┴────────────────────────────────────────────────────────────────
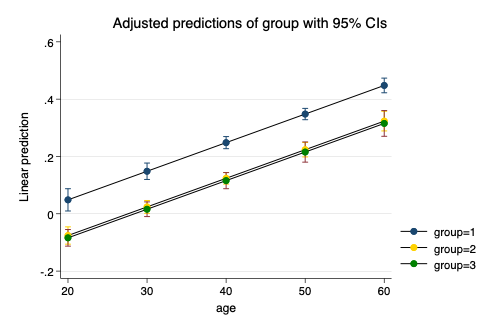
. marginsplot, scheme(michigan) // marginsplot Variables that uniquely identify margins: age group
. graph export mymarginplot1.png, width(500) replace
file /Users/agrogan/Desktop/newstuff/categorical/logistic-inherently-interactive/mymarginplot1.png
saved as PNG format

We see that, in accordance with the model that has no interactions, there are parallel regression lines for the different groups.
. logit outcome age i.group // logistic model with only main effects, no interactions
Iteration 0: log likelihood = -1366.0718
Iteration 1: log likelihood = -1117.4597
Iteration 2: log likelihood = -1076.5953
Iteration 3: log likelihood = -1075.0192
Iteration 4: log likelihood = -1075.0132
Iteration 5: log likelihood = -1075.0132
Logistic regression Number of obs = 3,000
LR chi2(3) = 582.12
Prob > chi2 = 0.0000
Log likelihood = -1075.0132 Pseudo R2 = 0.2131
─────────────┬────────────────────────────────────────────────────────────────
outcome │ Coefficient Std. err. z P>|z| [95% conf. interval]
─────────────┼────────────────────────────────────────────────────────────────
age │ .0904989 .006473 13.98 0.000 .0778121 .1031857
│
group │
2 │ -.7701431 .1262704 -6.10 0.000 -1.017629 -.5226576
3 │ -1.723107 .2740705 -6.29 0.000 -2.260275 -1.185938
│
_cons │ -5.150287 .3293441 -15.64 0.000 -5.79579 -4.504784
─────────────┴────────────────────────────────────────────────────────────────
. margins group, at(age = (20(10)60)) // calculate margins
Adjusted predictions Number of obs = 3,000
Model VCE: OIM
Expression: Pr(outcome), predict()
1._at: age = 20
2._at: age = 30
3._at: age = 40
4._at: age = 50
5._at: age = 60
─────────────┬────────────────────────────────────────────────────────────────
│ Delta-method
│ Margin std. err. z P>|z| [95% conf. interval]
─────────────┼────────────────────────────────────────────────────────────────
_at#group │
1 1 │ .0342139 .0067462 5.07 0.000 .0209916 .0474362
1 2 │ .0161357 .0030183 5.35 0.000 .0102199 .0220515
1 3 │ .0062842 .0017771 3.54 0.000 .0028011 .0097672
2 1 │ .0805187 .0106928 7.53 0.000 .0595612 .1014761
2 2 │ .0389606 .0052426 7.43 0.000 .0286854 .0492359
2 3 │ .0153915 .0039878 3.86 0.000 .0075756 .0232074
3 1 │ .1779452 .01342 13.26 0.000 .1516424 .2042479
3 2 │ .0910836 .0088552 10.29 0.000 .0737278 .1084394
3 3 │ .0372035 .0091939 4.05 0.000 .0191838 .0552233
4 1 │ .3485673 .0149823 23.27 0.000 .3192025 .377932
4 2 │ .1985334 .0171799 11.56 0.000 .1648614 .2322054
4 3 │ .0871891 .0211918 4.11 0.000 .0456539 .1287243
5 1 │ .5694594 .0228297 24.94 0.000 .5247141 .6142047
5 2 │ .3797765 .033522 11.33 0.000 .3140745 .4454784
5 3 │ .19101 .0448654 4.26 0.000 .1030754 .2789447
─────────────┴────────────────────────────────────────────────────────────────
. marginsplot, scheme(michigan) // marginsplot Variables that uniquely identify margins: age group
. graph export mymarginplot2.png, width(500) replace
file /Users/agrogan/Desktop/newstuff/categorical/logistic-inherently-interactive/mymarginplot2.png
saved as PNG format
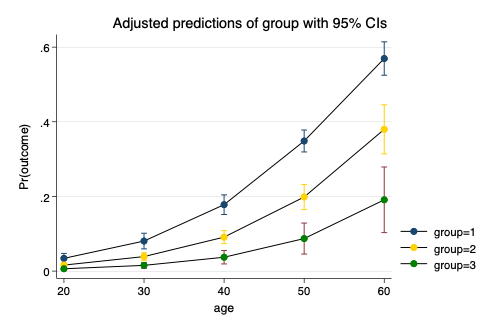
We see that, despite with the model that has no interactions, there are non-parallel (and non-linear) regression lines for the different groups.