Histogram of SES
. graph export myhistogram.png, width(1000) replace
(file /Users/agrogan/Desktop/newstuff/categorical/multilevel/myhistogram.png written
> in PNG format)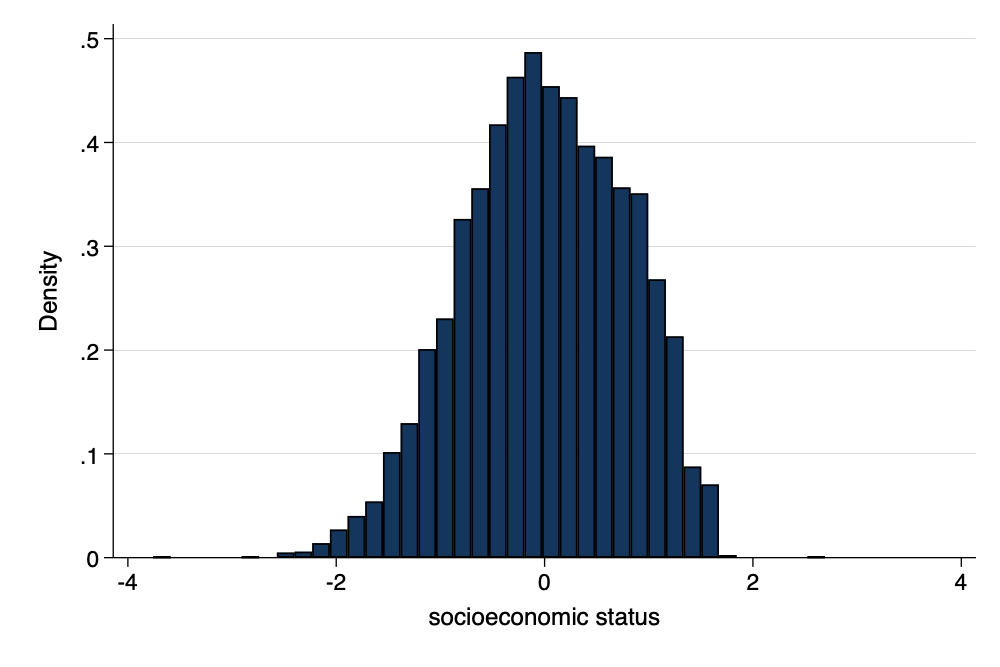
Histogram of SES
Andy Grogan-Kaylor
Andy Grogan-Kaylor
12 Feb 2021 17:21:48
. describe
Contains data from hsb.dta
obs: 7,185
vars: 7 27 Oct 2020 21:35
────────────────────────────────────────────────────────────────────────────────────
storage display value
variable name type format label variable label
────────────────────────────────────────────────────────────────────────────────────
female byte %8.0g female
ses float %9.0g socioeconomic status
mathach float %9.0g math achievement
size int %8.0g school size
sector byte %8.0g Catholic vs. Public
schoolid float %9.0g School ID
mathgroup float %9.0g math group (Hi / Lo)
────────────────────────────────────────────────────────────────────────────────────
Sorted by: . summarize
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
female │ 7,185 .5281837 .4992398 0 1
ses │ 7,185 .0001434 .7793552 -3.758 2.692
mathach │ 7,185 12.74785 6.878246 -2.832 24.993
size │ 7,185 1056.862 604.1725 100 2713
sector │ 7,185 .4931106 .4999873 0 1
─────────────┼─────────────────────────────────────────────────────────
schoolid │ 7,185 5277.898 2499.578 1224 9586
mathgroup │ 7,185 .5000696 .5000348 0 1. graph export myhistogram.png, width(1000) replace
(file /Users/agrogan/Desktop/newstuff/categorical/multilevel/myhistogram.png written
> in PNG format)
Histogram of SES
. summarize ses meanses
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
ses │ 7,185 .0001434 .7793552 -3.758 2.692
meanses │ 7,185 .0001434 .4135432 -1.193946 .8249825. twoway scatter ses meanses, msize(vsmall) ///
> title("SES and Mean SES Are Correlated") sub("But Not Equivalent") ///
> scheme(michigan). graph export myscatter.png, width(1000) replace
(file /Users/agrogan/Desktop/newstuff/categorical/multilevel/myscatter.png written i
> n PNG format)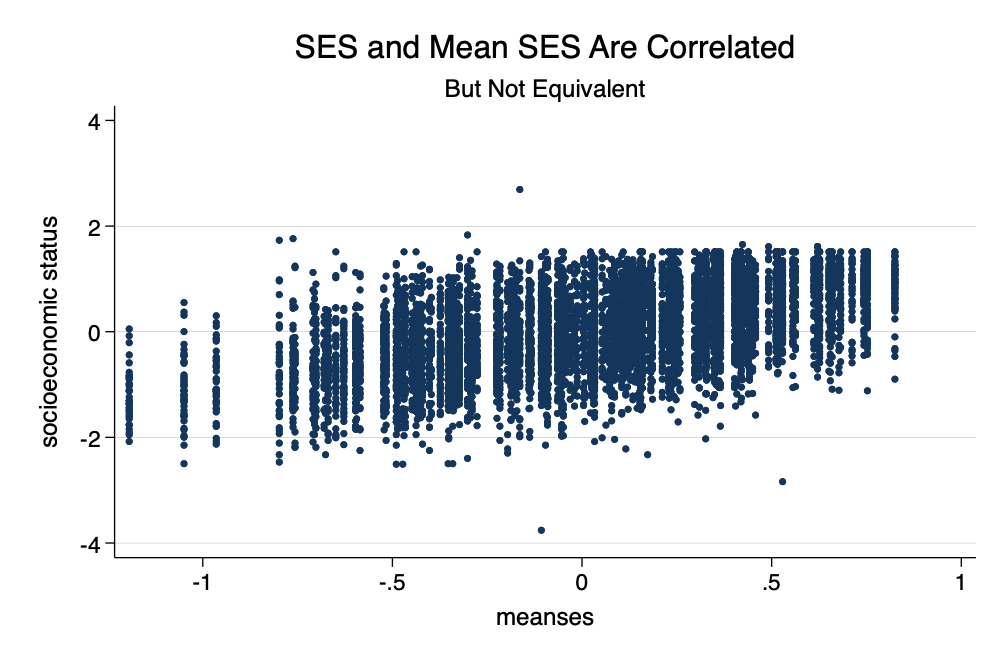
Scatterplot of SES and Mean SES by School
. melogit mathgroup female ses meanses size sector || schoolid:
Fitting fixed-effects model:
Iteration 0: log likelihood = -4510.2199
Iteration 1: log likelihood = -4507.2385
Iteration 2: log likelihood = -4507.2365
Iteration 3: log likelihood = -4507.2365
Refining starting values:
Grid node 0: log likelihood = -4500.0458
Fitting full model:
Iteration 0: log likelihood = -4500.0458 (not concave)
Iteration 1: log likelihood = -4464.0398
Iteration 2: log likelihood = -4456.1438
Iteration 3: log likelihood = -4455.9091
Iteration 4: log likelihood = -4455.9081
Iteration 5: log likelihood = -4455.9081
Mixed-effects logistic regression Number of obs = 7,185
Group variable: schoolid Number of groups = 160
Obs per group:
min = 14
avg = 44.9
max = 67
Integration method: mvaghermite Integration pts. = 7
Wald chi2(5) = 483.33
Log likelihood = -4455.9081 Prob > chi2 = 0.0000
─────────────┬────────────────────────────────────────────────────────────────
mathgroup │ Coef. Std. Err. z P>|z| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
female │ -.32004 .0571132 -5.60 0.000 -.4319798 -.2081003
ses │ .6061583 .0398911 15.20 0.000 .5279733 .6843434
meanses │ .8865231 .1199975 7.39 0.000 .6513323 1.121714
size │ .0001412 .0000777 1.82 0.069 -.0000111 .0002936
sector │ .4156577 .1017318 4.09 0.000 .2162671 .6150483
_cons │ -.1954753 .1244737 -1.57 0.116 -.4394392 .0484886
─────────────┼────────────────────────────────────────────────────────────────
schoolid │
var(_cons)│ .1822203 .0351234 .1248895 .265869
─────────────┴────────────────────────────────────────────────────────────────
LR test vs. logistic model: chibar2(01) = 102.66 Prob >= chibar2 = 0.0000. melogit, or
Mixed-effects logistic regression Number of obs = 7,185
Group variable: schoolid Number of groups = 160
Obs per group:
min = 14
avg = 44.9
max = 67
Integration method: mvaghermite Integration pts. = 7
Wald chi2(5) = 483.33
Log likelihood = -4455.9081 Prob > chi2 = 0.0000
─────────────┬────────────────────────────────────────────────────────────────
mathgroup │ Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
female │ .72612 .041471 -5.60 0.000 .6492225 .8121256
ses │ 1.833375 .0731353 15.20 0.000 1.695493 1.98247
meanses │ 2.426678 .2911952 7.39 0.000 1.918095 3.070111
size │ 1.000141 .0000777 1.82 0.069 .9999889 1.000294
sector │ 1.515367 .154161 4.09 0.000 1.241434 1.849746
_cons │ .8224437 .1023726 -1.57 0.116 .6443977 1.049683
─────────────┼────────────────────────────────────────────────────────────────
schoolid │
var(_cons)│ .1822203 .0351234 .1248895 .265869
─────────────┴────────────────────────────────────────────────────────────────
Note: Estimates are transformed only in the first equation.
Note: _cons estimates baseline odds (conditional on zero random effects).
LR test vs. logistic model: chibar2(01) = 102.66 Prob >= chibar2 = 0.0000. estat icc
Residual intraclass correlation
─────────────────────────────┬────────────────────────────────────────────────
Level │ ICC Std. Err. [95% Conf. Interval]
─────────────────────────────┼────────────────────────────────────────────────
schoolid │ .0524815 .009585 .0365734 .0747718
─────────────────────────────┴────────────────────────────────────────────────. twoway (function y = logistic(x), range(-5 5)) /// first school; random intercept
> 0
> (function y = logistic(x + 1), range(-5 5)) /// second school; random intercept 1
> (function y = logistic(x - 1), range(-5 5)), /// third school; random intercept -1
> title("Three Hypothetical Schools") ///
> sub("With Different Random Intercepts") ///
> legend(order(1 "random intercept 0" 2 "random intercept +1" 3 "random intercept -1
> ")) ///
> scheme(michigan). graph export myMLM.png, width(1000) replace
(file /Users/agrogan/Desktop/newstuff/categorical/multilevel/myMLM.png written in PN
> G format)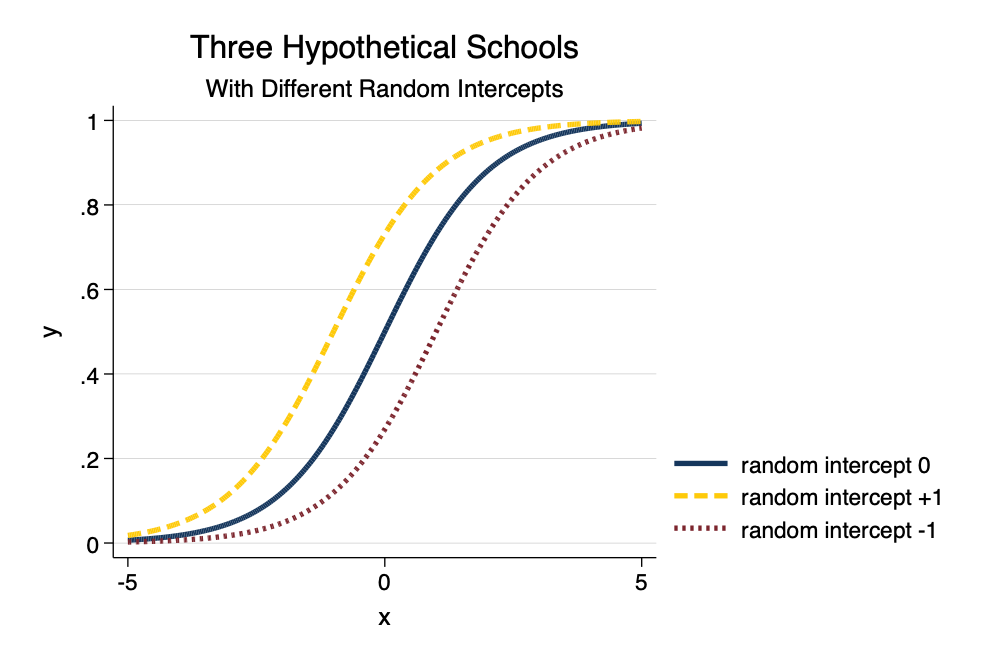
Simulated MLM of School Data
Multilevel modeling is useful in a number of situations with clustering.
| Model | Clustering or Nesting |
|---|---|
| Nested or clustered cross-sectional data | People inside social units such as families, classrooms, schools or neighborhoods, … inside states, countries, etc. |
| Longitudinal data | Measurement occasions inside people (multiple time points; different people have very different time points) |
| Meta-Analysis | People inside multiple studies concerning a particular outcome |
| Meta-Analysis of Multiple Outcomes | People inside multiple studies concerning different outcomes |
| Dyadic analysis (e.g. couples; parent and child in family) | People inside dyads |
| Combinations of these approaches |
Mathematics is the art of giving the same name to different things. —Henri Poincaré
Our notation for logistic regression model is:
\[ \ln \Big( \frac{p(\text{outcome})}{1 - p(\text{outcome})} \Big) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... \]
which after exponentiating both sides, and some rearrangement, can be written:
\[ p(\text{outcome}) = \frac{e^{\beta_0 + \beta_1 x_1 + \beta_2 x_2 + ...}}{1 +e^{\beta_0 + \beta_1 x_1 + \beta_2 x_2 + ...}} = \]
\[ F(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + ...) \]
where \(F(z) = \frac{e^z}{1 + e^z}\), which is the logistic distribution.
So in adapting this notation for the multilevel context, we are ultimately going to write the notation for the multilevel logistic regression model as:
\(p(\text{outcome} | \text{unique intercept for each unit}) = F(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + u_{0j})\)
Multilevel models have complicated likelihoods. As we move toward the middle to end of this table, models may have difficulty converging.
| Single Level Command | Multilevel Command |
|---|---|
regress y x |
mixed y x || id: |
logit y x |
melogit y x || id: |
ologit y x |
meologit y x || id: |
mlogit y x |
gsem... |
poisson y x |
mepoisson y x || id: |
nbreg y x |
menbreg y x || id: |