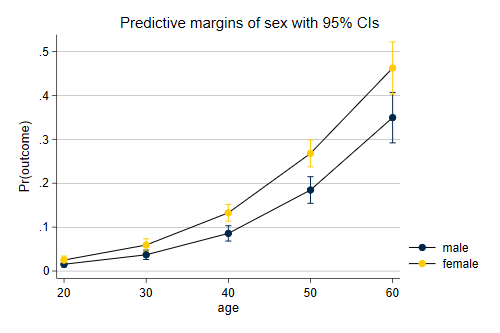
Graph of Predicted Margins
predict and marginsOdds ratios, or coefficients showing the association of the independent variables with the log odds, represent the most immediate output of a logistic regression. However, for a variety of reasons, it may make sense to not only report odds ratios, but also to investigate predicted probabilities.
We start by obtaining simulated data from StataCorp.
. clear all
. graph close _all
. use http://www.stata-press.com/data/r15/margex, clear (Artificial data for margins)
The variables are as follows:
. describe
Contains data from http://www.stata-press.com/data/r15/margex.dta
Observations: 3,000 Artificial data for margins
Variables: 11 27 Nov 2016 14:27
────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Variable Storage Display Value
name type format label Variable label
────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
y float %6.1f
outcome byte %2.0f
sex byte %6.0f sexlbl
group byte %2.0f
age float %3.0f
distance float %6.2f
ycn float %6.1f
yc float %6.1f
treatment byte %2.0f
agegroup byte %8.0g agelab
arm byte %8.0g
────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Sorted by: group
logit)We then run a logistic regression model in which outcome is the dependent variable. sex, age and group are the independent variables.
. logit outcome i.sex c.age i.group, or
Iteration 0: log likelihood = -1366.0718
Iteration 1: log likelihood = -1111.4595
Iteration 2: log likelihood = -1069.588
Iteration 3: log likelihood = -1068
Iteration 4: log likelihood = -1067.9941
Iteration 5: log likelihood = -1067.9941
Logistic regression Number of obs = 3,000
LR chi2(4) = 596.16
Prob > chi2 = 0.0000
Log likelihood = -1067.9941 Pseudo R2 = 0.2182
─────────────┬────────────────────────────────────────────────────────────────
outcome │ Odds ratio Std. err. z P>|z| [95% conf. interval]
─────────────┼────────────────────────────────────────────────────────────────
sex │
female │ 1.64734 .221973 3.70 0.000 1.26499 2.145258
age │ 1.09444 .0070921 13.93 0.000 1.080628 1.108429
│
group │
2 │ .5568139 .0751806 -4.34 0.000 .4273478 .725502
3 │ .2566074 .0747822 -4.67 0.000 .1449462 .4542885
│
_cons │ .0038757 .0013558 -15.87 0.000 .0019524 .0076933
─────────────┴────────────────────────────────────────────────────────────────
Note: _cons estimates baseline odds.
margins)We use the margins command to estimate predicted probabilities at different values of sex and age.
. margins sex, at(age = (20 30 40 50 60))
Predictive margins Number of obs = 3,000
Model VCE: OIM
Expression: Pr(outcome), predict()
1._at: age = 20
2._at: age = 30
3._at: age = 40
4._at: age = 50
5._at: age = 60
─────────────┬────────────────────────────────────────────────────────────────
│ Delta-method
│ Margin std. err. z P>|z| [95% conf. interval]
─────────────┼────────────────────────────────────────────────────────────────
_at#sex │
1#male │ .0153934 .0031264 4.92 0.000 .0092657 .0215211
1#female │ .0250609 .0046143 5.43 0.000 .0160171 .0341048
2#male │ .0369626 .0054588 6.77 0.000 .0262635 .0476616
2#female │ .0592151 .0072711 8.14 0.000 .0449639 .0734663
3#male │ .0856677 .0088815 9.65 0.000 .0682603 .1030751
3#female │ .1325688 .0097333 13.62 0.000 .1134919 .1516458
4#male │ .1844578 .015461 11.93 0.000 .1541547 .2147608
4#female │ .2677423 .015609 17.15 0.000 .2371493 .2983353
5#male │ .349279 .029326 11.91 0.000 .2918012 .4067569
5#female │ .4622129 .0303129 15.25 0.000 .4028007 .5216251
─────────────┴────────────────────────────────────────────────────────────────
marginsplot)margins provides a lot of results, which can be difficult to understand. Therefore, we use marginsplot to plot these margins results. The key command is marginsplot, which could be used on its own. I have simply added the Michigan graph scheme, as well as some options to improve the graphic design of the plot.
. marginsplot, scheme(michigan) Variables that uniquely identify margins: age sex
. graph export mymarginsplot.png, width(500) replace file mymarginsplot.png saved as PNG format

Graph of Predicted Margins
predict)Predicted probabilities are each participant's individual predicted probability of experiencing depression based upon the independent variables included in the model. We often denote such predicted probabilities with \(\hat{y}\)
. predict yhat (option pr assumed; Pr(outcome))
yhat is a variable in the data, just like any other variable, and we can summarize and graph it.
. twoway (lowess yhat age if sex == 0) ///
> (lowess yhat age if sex == 1), ///
> title("Predicted Probabilities of Outcome") ///
> legend(order(1 "male" 2 "female")) ///
> scheme(michigan)
. graph export mytwoway.png, width(500) replace file mytwoway.png saved as PNG format

Graph of Predicted Probabilities
margins, Posting ResultsWe again employ the margins command, this time using the post option so that the results of the margins command are posted as an estimation result. This will allow us to employ the test command to statistically test different margins against each other.
. margins sex, at(age = (20 30 40 50 60)) post
Predictive margins Number of obs = 3,000
Model VCE: OIM
Expression: Pr(outcome), predict()
1._at: age = 20
2._at: age = 30
3._at: age = 40
4._at: age = 50
5._at: age = 60
─────────────┬────────────────────────────────────────────────────────────────
│ Delta-method
│ Margin std. err. z P>|z| [95% conf. interval]
─────────────┼────────────────────────────────────────────────────────────────
_at#sex │
1#male │ .0153934 .0031264 4.92 0.000 .0092657 .0215211
1#female │ .0250609 .0046143 5.43 0.000 .0160171 .0341048
2#male │ .0369626 .0054588 6.77 0.000 .0262635 .0476616
2#female │ .0592151 .0072711 8.14 0.000 .0449639 .0734663
3#male │ .0856677 .0088815 9.65 0.000 .0682603 .1030751
3#female │ .1325688 .0097333 13.62 0.000 .1134919 .1516458
4#male │ .1844578 .015461 11.93 0.000 .1541547 .2147608
4#female │ .2677423 .015609 17.15 0.000 .2371493 .2983353
5#male │ .349279 .029326 11.91 0.000 .2918012 .4067569
5#female │ .4622129 .0303129 15.25 0.000 .4028007 .5216251
─────────────┴────────────────────────────────────────────────────────────────
margins with coeflegendWe follow up by using the margins command with the coeflegend option to see the way in which Stata has labeled the different margins.
. margins, coeflegend
Predictive margins Number of obs = 3,000
Model VCE: OIM
Expression: Pr(outcome), predict()
1._at: age = 20
2._at: age = 30
3._at: age = 40
4._at: age = 50
5._at: age = 60
─────────────┬────────────────────────────────────────────────────────────────
│ Margin Legend
─────────────┼────────────────────────────────────────────────────────────────
_at#sex │
1#male │ .0153934 _b[1bn._at#0bn.sex]
1#female │ .0250609 _b[1bn._at#1.sex]
2#male │ .0369626 _b[2._at#0bn.sex]
2#female │ .0592151 _b[2._at#1.sex]
3#male │ .0856677 _b[3._at#0bn.sex]
3#female │ .1325688 _b[3._at#1.sex]
4#male │ .1844578 _b[4._at#0bn.sex]
4#female │ .2677423 _b[4._at#1.sex]
5#male │ .349279 _b[5._at#0bn.sex]
5#female │ .4622129 _b[5._at#1.sex]
─────────────┴────────────────────────────────────────────────────────────────
Lastly, we can test margins against eachother, e.g. the margins at age 20 for men and women, and again at age 50 for men and women.
. test _b[1bn._at#0bn.sex] = _b[1bn._at#1.sex] // male and female at age 20
( 1) 1bn._at#0bn.sex - 1bn._at#1.sex = 0
chi2( 1) = 10.62
Prob > chi2 = 0.0011
. test _b[4._at#0bn.sex] = _b[4._at#1.sex] // male and female at age 50
( 1) 4._at#0bn.sex - 4._at#1.sex = 0
chi2( 1) = 13.85
Prob > chi2 = 0.0002