The Stata Interface
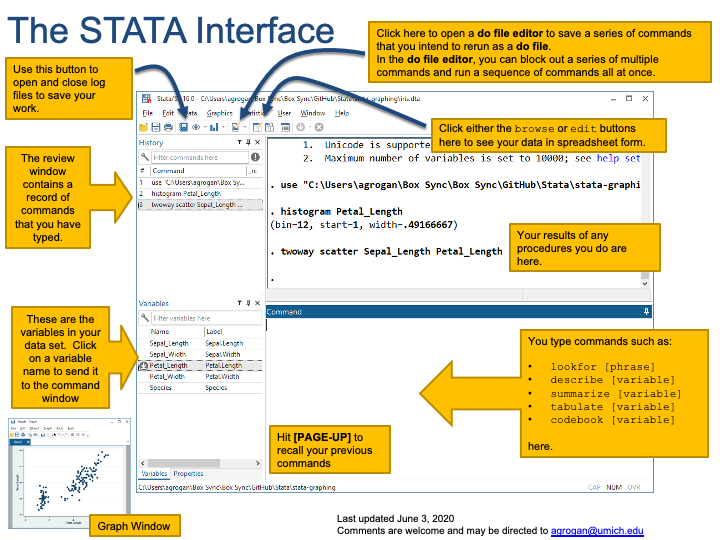
The Stata Interface
Andy Grogan-Kaylor
Andy Grogan-Kaylor
2 Sep 2021
do_something to_variable(s), options
Quite often the default options are so well chosen that you do not need to specify any options.
use mydata.dtasummarize // descriptive statisticskeep x1 x2 x3 // keep only selected variableslist x1 x2 x3 in 1/10 // list cases for selected variablesbrowse // look at datalookfor [word] // look for variables with a particular word
The Stata Interface
. summarize
Variable │ Obs Mean Std. dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
ID │ 521 2965.449 1158.32 1005 4989
age │ 521 28.0438 7.047373 18.05584 45.45653
gender │ 521 1.821497 .7549825 1 3
program │ 521 2.197697 .7973963 1 4
mental_hea~1 │ 521 95.11707 5.161698 80.93709 108.5736
─────────────┼─────────────────────────────────────────────────────────
mental_hea~2 │ 521 98.87066 7.423767 79.57518 118.2272
latitude │ 521 42.25321 .1027698 41.99847 42.6237
longitude │ 521 -83.74921 .0987047 -84.04328 -83.42666. summarize age, detail
age
─────────────────────────────────────────────────────────────
Percentiles Smallest
1% 18.17739 18.05584
5% 18.72159 18.05992
10% 19.54324 18.10945 Obs 521
25% 22.37428 18.13374 Sum of wgt. 521
50% 26.61352 Mean 28.0438
Largest Std. dev. 7.047373
75% 32.88188 44.35607
90% 38.46387 44.78399 Variance 49.66547
95% 41.26977 45.30344 Skewness .5501433
99% 44.16425 45.45653 Kurtosis 2.317297Some programs, e.g. R make you search for standard deviation. With Stata, sd is easily accessible with
summarize.
. graph export myhistogram.png, width(500) replace
file
/Users/agrogan/Desktop/GitHub/newstuff/categorical/review-stats-intro-stata/myhistogram.
> png saved as PNG format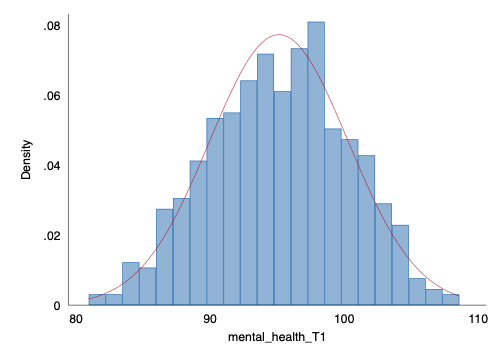
histogram of mental health
. graph export myscatter.png, width(500) replace
file
/Users/agrogan/Desktop/GitHub/newstuff/categorical/review-stats-intro-stata/myscatter.pn
> g saved as PNG format
scatterplot of age and mental health
. graph export mybargraph.png, width(500) replace
file
/Users/agrogan/Desktop/GitHub/newstuff/categorical/review-stats-intro-stata/mybargraph.p
> ng saved as PNG format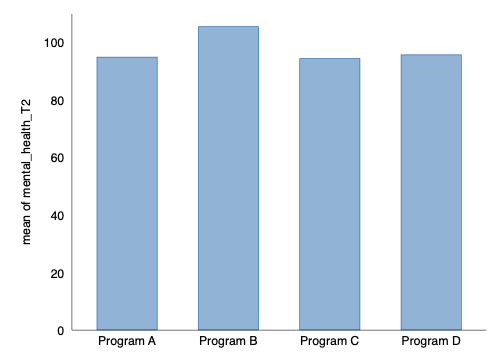
bar graph of mental health at time 2
. ttest mental_health_T2, by(program)
Two-sample t test with equal variances
─────────┬────────────────────────────────────────────────────────────────────
Group │ Obs Mean Std. err. Std. dev. [95% conf. interval]
─────────┼────────────────────────────────────────────────────────────────────
Program │ 111 94.7963 .4969934 5.23615 93.81138 95.78123
Program │ 209 105.3512 .3562424 5.150136 104.6489 106.0535
─────────┼────────────────────────────────────────────────────────────────────
Combined │ 320 101.69 .4033737 7.215767 100.8964 102.4836
─────────┼────────────────────────────────────────────────────────────────────
diff │ -10.55491 .6083793 -11.75187 -9.357953
─────────┴────────────────────────────────────────────────────────────────────
diff = mean(Program) - mean(Program) t = -17.3492
H0: diff = 0 Degrees of freedom = 318
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0000 Pr(|T| > |t|) = 0.0000 Pr(T > t) = 1.0000. oneway mental_health_T2 program, tabulate // oneway analysis of variance
│ Summary of mental_health_T2
program │ Mean Std. dev. Freq.
────────────┼────────────────────────────────────
Program A │ 94.796305 5.2361502 111
Program B │ 105.35121 5.1501362 209
Program C │ 94.299149 5.2002254 188
Program D │ 95.582917 5.6199143 13
────────────┼────────────────────────────────────
Total │ 98.870656 7.4237673 521
Analysis of variance
Source SS df MS F Prob > F
────────────────────────────────────────────────────────────────────────
Between groups 14689.6155 3 4896.53849 181.23 0.0000
Within groups 13968.791 517 27.0189382
────────────────────────────────────────────────────────────────────────
Total 28658.4065 520 55.1123202
Bartlett's equal-variances test: chi2(3) = 0.1991 Prob>chi2 = 0.978Importantly,
,tabulategives us a table of results.
. regress mental_health_T2 mental_health_T1 i.program
Source │ SS df MS Number of obs = 521
─────────────┼────────────────────────────────── F(4, 516) = 135.94
Model │ 14704.3725 4 3676.09313 Prob > F = 0.0000
Residual │ 13954.034 516 27.0427015 R-squared = 0.5131
─────────────┼────────────────────────────────── Adj R-squared = 0.5093
Total │ 28658.4065 520 55.1123202 Root MSE = 5.2003
─────────────────┬────────────────────────────────────────────────────────────────
mental_health_T2 │ Coefficient Std. err. t P>|t| [95% conf. interval]
─────────────────┼────────────────────────────────────────────────────────────────
mental_health_T1 │ -.0327405 .044321 -0.74 0.460 -.1198123 .0543314
│
program │
Program B │ 10.57171 .6111758 17.30 0.000 9.371008 11.77241
Program C │ -.494409 .6224837 -0.79 0.427 -1.717323 .728505
Program D │ .7226213 1.526873 0.47 0.636 -2.27703 3.722272
│
_cons │ 97.90435 4.236239 23.11 0.000 89.58195 106.2267
─────────────────┴────────────────────────────────────────────────────────────────Instructor will draw this out.
. regress mental_health_T2 c.mental_health_T1##i.program
Source │ SS df MS Number of obs = 521
─────────────┼────────────────────────────────── F(7, 513) = 77.65
Model │ 14743.6327 7 2106.23324 Prob > F = 0.0000
Residual │ 13914.7738 513 27.1243155 R-squared = 0.5145
─────────────┼────────────────────────────────── Adj R-squared = 0.5078
Total │ 28658.4065 520 55.1123202 Root MSE = 5.2081
───────────────────────────┬────────────────────────────────────────────────────────────────
mental_health_T2 │ Coefficient Std. err. t P>|t| [95% conf. interval]
───────────────────────────┼────────────────────────────────────────────────────────────────
mental_health_T1 │ .0038108 .0940124 0.04 0.968 -.1808858 .1885074
│
program │
Program B │ 14.13882 11.07298 1.28 0.202 -7.615155 35.89279
Program C │ 2.227825 11.6862 0.19 0.849 -20.73087 25.18653
Program D │ 27.30439 22.3002 1.22 0.221 -16.50657 71.11535
│
program#c.mental_health_T1 │
Program B │ -.0375708 .1162481 -0.32 0.747 -.2659517 .1908101
Program C │ -.0286832 .1228833 -0.23 0.816 -.2700997 .2127332
Program D │ -.2851331 .2385022 -1.20 0.232 -.7536944 .1834281
│
_cons │ 94.43455 8.938253 10.57 0.000 76.87446 111.9946
───────────────────────────┴────────────────────────────────────────────────────────────────
Social Service Agency Data