Background

Risks and Odds are different but related quantities. It it important to understand how each is mathematically defined and to understand what each quantity implies. In some cases, the odds may overstate the risk.

Setup

. clear all

We are going to set up a table with 10 rows of information.

. set obs 10 // 10 rows of information
Number of observations (_N) was 0, now 10.

. generate occasions = 100 // 100 hypothetical occasions

In each row of the table our event of interest happened a different number of times.

In the code below we make use of Stata’s special variable for the row number of a data set: _n.

. generate event_happened = _n * 10

As a result, the event of interest didn’t happen \(100 - \text{happened}\) times.

. generate event_didnt_happen = 100 - event_happened

As you think through the rest of this example, it might be worth giving yourself a concrete example of the event of interest. What is a concrete example of a good thing that might happen, or a bad thing that might happen?

Our Table of Information So Far

Let’s list out our table of information so far:

. list, abbreviate(20)

     ┌─────────────────────────────────────────────────┐
     │ occasions   event_happened   event_didnt_happen │
     ├─────────────────────────────────────────────────┤
  1. │       100               10                   90 │
  2. │       100               20                   80 │
  3. │       100               30                   70 │
  4. │       100               40                   60 │
  5. │       100               50                   50 │
     ├─────────────────────────────────────────────────┤
  6. │       100               60                   40 │
  7. │       100               70                   30 │
  8. │       100               80                   20 │
  9. │       100               90                   10 │
 10. │       100              100                    0 │
     └─────────────────────────────────────────────────┘

Risk

Now let’s think about risk:

\[ \text{risk} = P(\text{event}) = \frac{\text{number of events that happened}}{\text{number of events that happened} + \text{number of events that didn't happen}} \]

. generate risk_event_happened = event_happened / (event_happened + event_didnt_happen
> )

There is also a risk that the event didn’t happen.

. generate risk_event_didnt_happen = event_didnt_happen / (event_happened + event_didn
> t_happen)

Odds

The odds are the probability that an event happened divided by the probability that it did not happen

\[ \text{odds} = \frac{P(\text{event happened})}{P(\text{event didn't happen})} \]

\[ = \frac{\frac{\text{number of events}}{\text{number of events} + \text{number of non-events}}}{\frac{\text{number of non-events}}{\text{number of events} + \text{number of non-events}}} \]

. generate odds = risk_event_happened / risk_event_didnt_happen
(1 missing value generated)

which incidentally reduces to

\[ = \frac{\text{number of events}}{\text{number of non-events}} \]

Look At Our Table Of Information

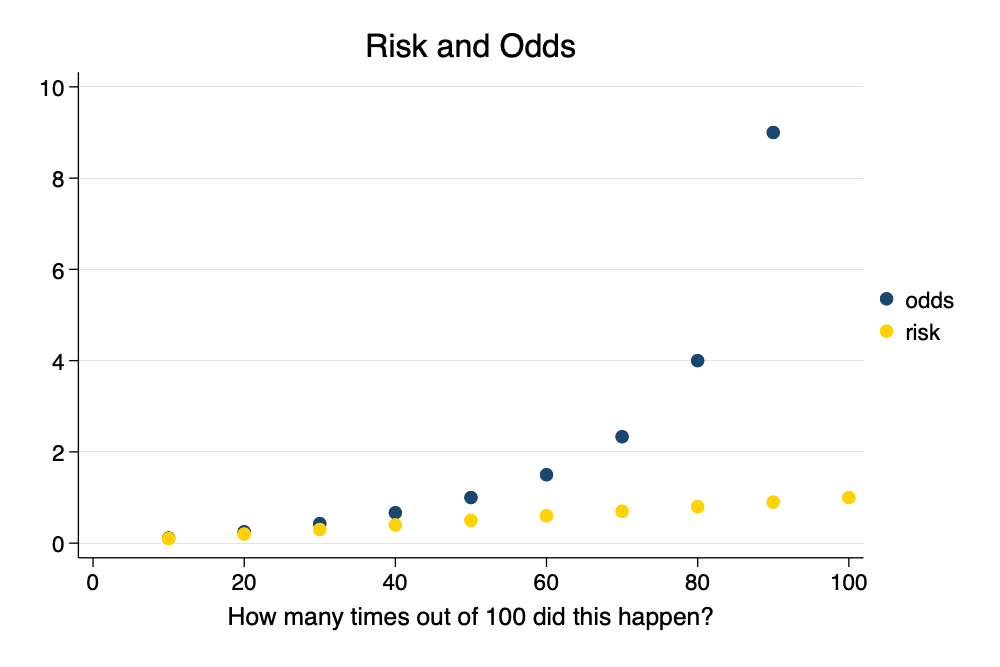
Let’s look at our table of information.

Notice how the odds start to overstate the risk, as the risk becomes more common.

. list event_happened ///
> risk_event_happened ///
> odds, ///
> abbreviate(20)

     ┌─────────────────────────────────────────────────┐
     │ event_happened   risk_event_happened       odds │
     ├─────────────────────────────────────────────────┤
  1. │             10                    .1   .1111111 │
  2. │             20                    .2        .25 │
  3. │             30                    .3   .4285715 │
  4. │             40                    .4   .6666666 │
  5. │             50                    .5          1 │
     ├─────────────────────────────────────────────────┤
  6. │             60                    .6        1.5 │
  7. │             70                    .7   2.333333 │
  8. │             80                    .8          4 │
  9. │             90                    .9          9 │
 10. │            100                     1          . │
     └─────────────────────────────────────────────────┘

We can even graph this.

. twoway scatter odds risk_event_happened event_happened, ///
> title("Risk and Odds") ///
> xtitle("How many times out of 100 did this happen?") ///
> scheme(michigan) ///
> legend(pos(3) order(1 "odds" 2 "risk"))

. quietly: graph export myscatter.png, width(1000) replace