Cox Proportional Hazards Model

Andy Grogan-Kaylor

Cox Proportional Hazards Model

Andy Grogan-Kaylor

12 Nov 2023

Introduction

“Survival analysis is a key technique in data-driven decision-making, which is now central to public interest because of COVID-19. Applying the correct technique for the specific question at hand is crucial for credible public health inferences. If you are interested in assessing how a risk factor or a potential treatment affects the progression of a disease—such as how long a patient takes to recover—then survival analysis techniques come into play. Survival analysis deeply respects the ultimate source of its data, often the disease experience or even the life and death of human patients. It seeks to exploit every last drop of information that this experience can render for saving lives—in particular, not only whether patients survived, but how long, and why. And it strives to do so with minimal assumptions, so that the data are truly driving the decision.”

—SAS Corporation

Cox Proportional Hazards Model

Formula for the Hazard

\(h(t)\) the rate of occurrence.

\[ h(t) = \lim_{\delta\to\infty} \frac{\text{probability of having an event before time } t + \delta}{\delta} \]

This definition per Johnson & Shih (2007).

\[ h(t) = h_0(t)e^{\beta_1 x1 + \beta_2 x_2 + etc.} \]

We don’t directly estimate the hazard, but estimate the effect of covariates on the hazard.

The event (birth, death, program entry, program departure) is coded as 1, so we are estimating the association of the covariates with event occurrence.

Cox Proportional Hazards Model in Stata

Using a data set referenced frequently in Stata help and Stata YouTube Videos

. clear all
. webuse drugtr // demonstration data set from Stata
(Patient survival in drug trial)

Setup of Data

. stset // show st setup of data
-> stset studytime, failure(died)

Survival-time data settings

         Failure event: died!=0 & died<.
Observed time interval: (0, studytime]
     Exit on or before: failure

──────────────────────────────────────────────────────────────────────────
         48  total observations
          0  exclusions
──────────────────────────────────────────────────────────────────────────
         48  observations remaining, representing
         31  failures in single-record/single-failure data
        744  total analysis time at risk and under observation
                                                At risk from t =         0
                                     Earliest observed entry t =         0
                                          Last observed exit t =        39
. describe // show variables in data

Contains data from https://www.stata-press.com/data/r18/drugtr.dta
 Observations:            48                  Patient survival in drug trial
    Variables:             8                  3 Mar 2022 02:12
───────────────────────────────────────────────────────────────────────────────────────
Variable      Storage   Display    Value
    name         type    format    label      Variable label
───────────────────────────────────────────────────────────────────────────────────────
studytime       byte    %8.0g                 Months to death or end of exp.
died            byte    %8.0g                 1 if patient died
drug            byte    %8.0g                 Drug type (0=placebo)
age             byte    %8.0g                 Patient's age at start of exp.
_st             byte    %8.0g                 1 if record is to be used; 0 otherwise
_d              byte    %8.0g                 1 if failure; 0 if censored
_t              byte    %10.0g                Analysis time when record ends
_t0             byte    %10.0g                Analysis time when record begins
───────────────────────────────────────────────────────────────────────────────────────
Sorted by:

Kaplan-Meier Survivor Function (per Gabriela Ortiz, Stata)

\[ S(t)=Pr(T>t) \]

. sts graph, scheme(michigan) // Kaplan-Meier Survivor Function

        Failure _d: died
  Analysis time _t: studytime
. graph export survival0.png, width(1000) replace
file
    /Users/agrogan/Desktop/GitHub/newstuff/categorical/survival-analysis-and-event-hi
    > story/survival0.png saved as PNG format
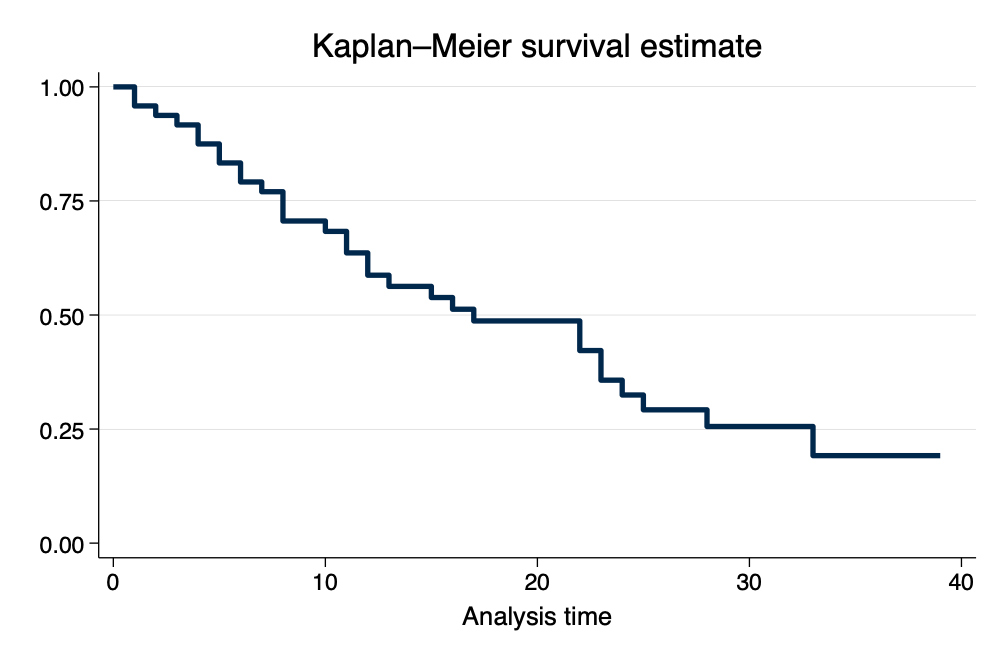
Kaplan-Meier Survivor Function
Kaplan-Meier Survivor Function

Cox Proportional Hazards Model

. stcox age drug // run Cox Proportional Hazards Model

        Failure _d: died
  Analysis time _t: studytime

Iteration 0:  Log likelihood = -99.911448
Iteration 1:  Log likelihood = -83.551879
Iteration 2:  Log likelihood = -83.324009
Iteration 3:  Log likelihood = -83.323546
Refining estimates:
Iteration 0:  Log likelihood = -83.323546

Cox regression with Breslow method for ties

No. of subjects =  48                                   Number of obs =     48
No. of failures =  31
Time at risk    = 744
                                                        LR chi2(2)    =  33.18
Log likelihood = -83.323546                             Prob > chi2   = 0.0000

─────────────┬────────────────────────────────────────────────────────────────
          _t │ Haz. ratio   Std. err.      z    P>|z|     [95% conf. interval]
─────────────┼────────────────────────────────────────────────────────────────
         age │   1.120325   .0417711     3.05   0.002     1.041375     1.20526
        drug │   .1048772   .0477017    -4.96   0.000     .0430057    .2557622
─────────────┴────────────────────────────────────────────────────────────────

Graph Survival Curves

. stcurve, survival scheme(michigan) // survival curve
note: function evaluated at overall means of covariates.
. graph export survival1.png, width(1000) replace
file
    /Users/agrogan/Desktop/GitHub/newstuff/categorical/survival-analysis-and-event-hi
    > story/survival1.png saved as PNG format
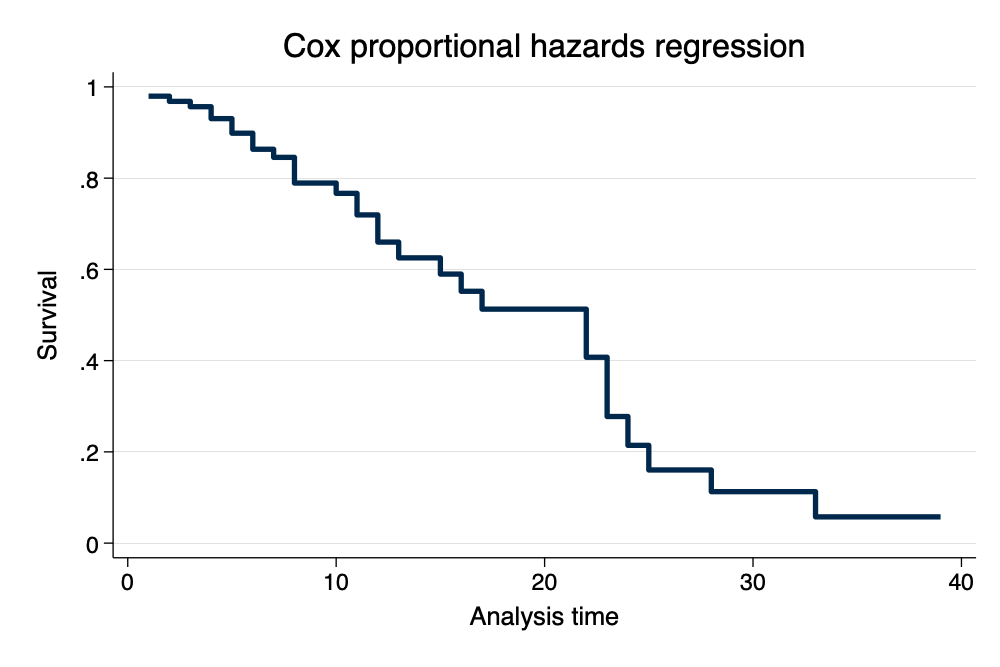
Survival Curve
Survival Curve
. stcurve, survival at1(drug=0) at2(drug=1) scheme(michigan) // survival curve by group
note: function evaluated at specified values of selected covariates and overall means
      of other covariates (if any).
. graph export survival2.png, width(1000) replace
file
    /Users/agrogan/Desktop/GitHub/newstuff/categorical/survival-analysis-and-event-hi
    > story/survival2.png saved as PNG format
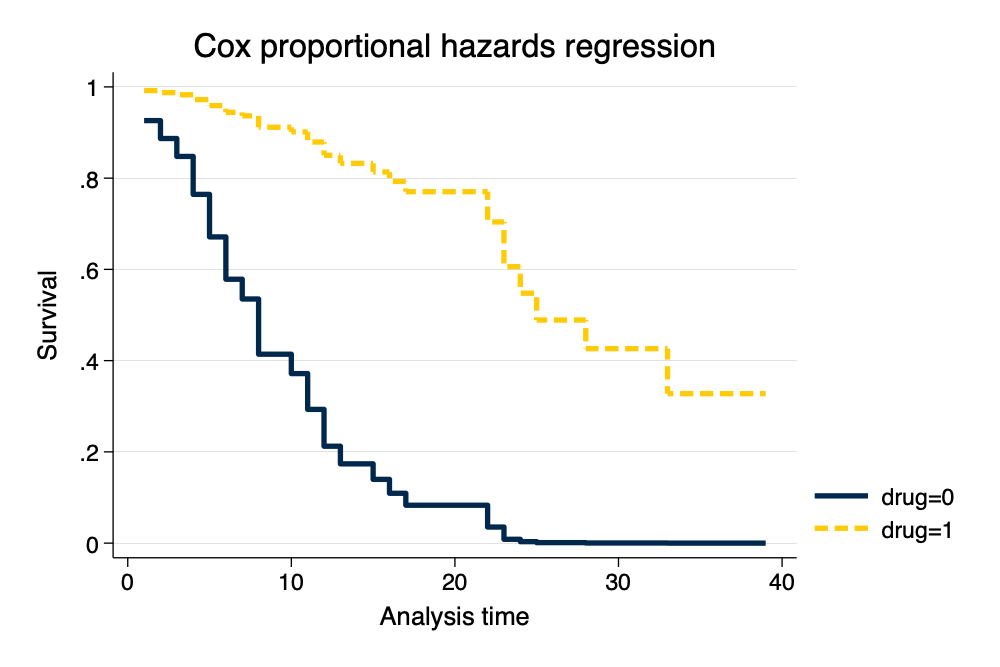
Survival Curve by Drug Group
Survival Curve by Drug Group

Proportional Hazards Assumption

. estat phtest // formal test of PH assumption

Test of proportional-hazards assumption

Time function: Analysis time
─────────────┬──────────────────────────────────
             │     chi2       df       Prob>chi2
─────────────┼──────────────────────────────────
 Global test │     0.43        2          0.8064
─────────────┴──────────────────────────────────
. stphplot, by(drug) scheme(michigan) // graphical test of PH assumption

        Failure _d: died
  Analysis time _t: studytime
. graph export ph.png, width(1000) replace
file
    /Users/agrogan/Desktop/GitHub/newstuff/categorical/survival-analysis-and-event-hi
    > story/ph.png saved as PNG format
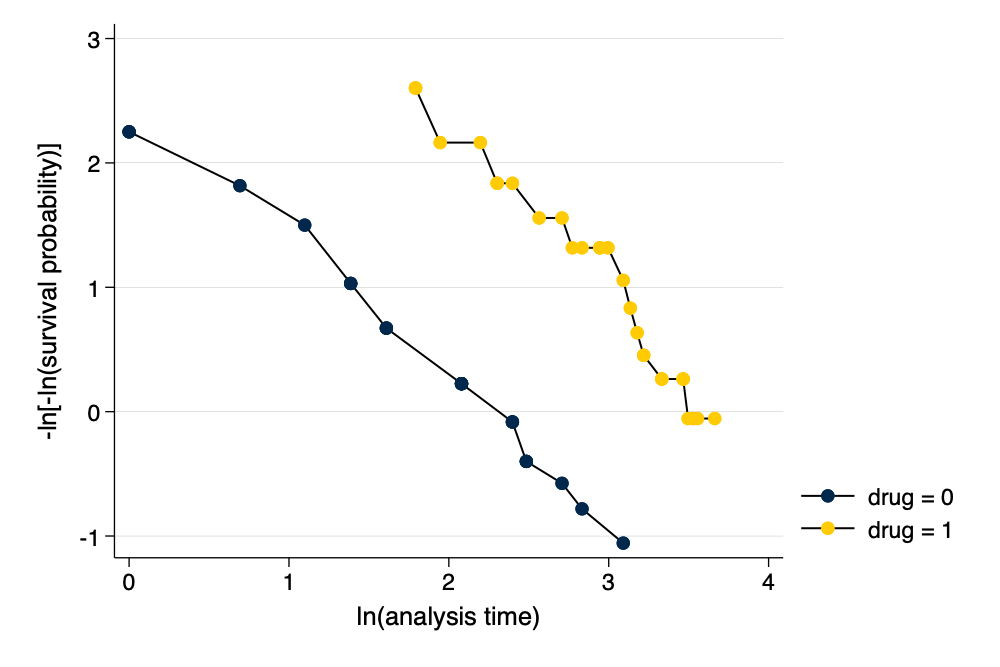
Graphical Assessment of Proportional Hazards Assumptions
Graphical Assessment of Proportional Hazards Assumptions

References

Johnson, L. L., & Shih, J. H. (2007). CHAPTER 20 - An Introduction to Survival Analysis (J. I. Gallin & F. P. Ognibene, eds.). https://doi.org/https://doi.org/10.1016/B978-012369440-9/50024-4

Ragnar Frisch Centre for Economic Research (2020). Event History Analysis, Survival Analysis, Duration Analysis ,Transition Data Analysis, Hazard Rate Analysis. Oslo, Norway.