Likelihood and Log Likelihood

1 Background

The likelihood is the probability that a given set of parameters would give rise to a given data set.

Formally, the likelihood is a product of probabilities.

\[\mathscr{L}(\beta) = \prod p(\beta | x, y) \tag{1}\]

2 Maximum Likelihood Estimation

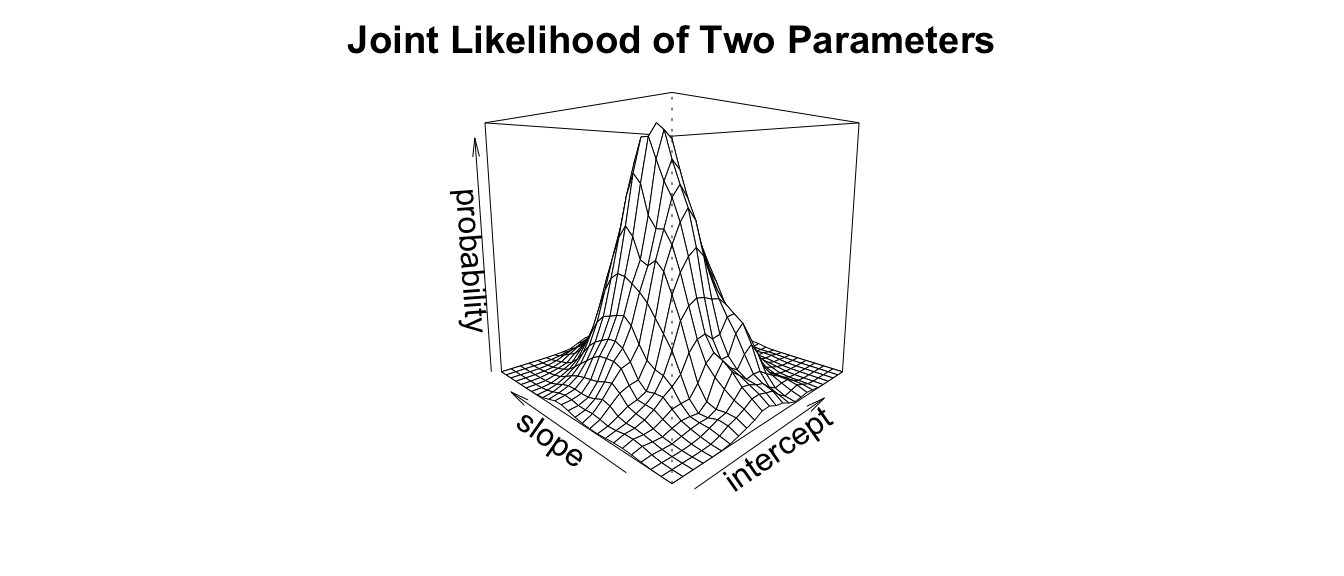
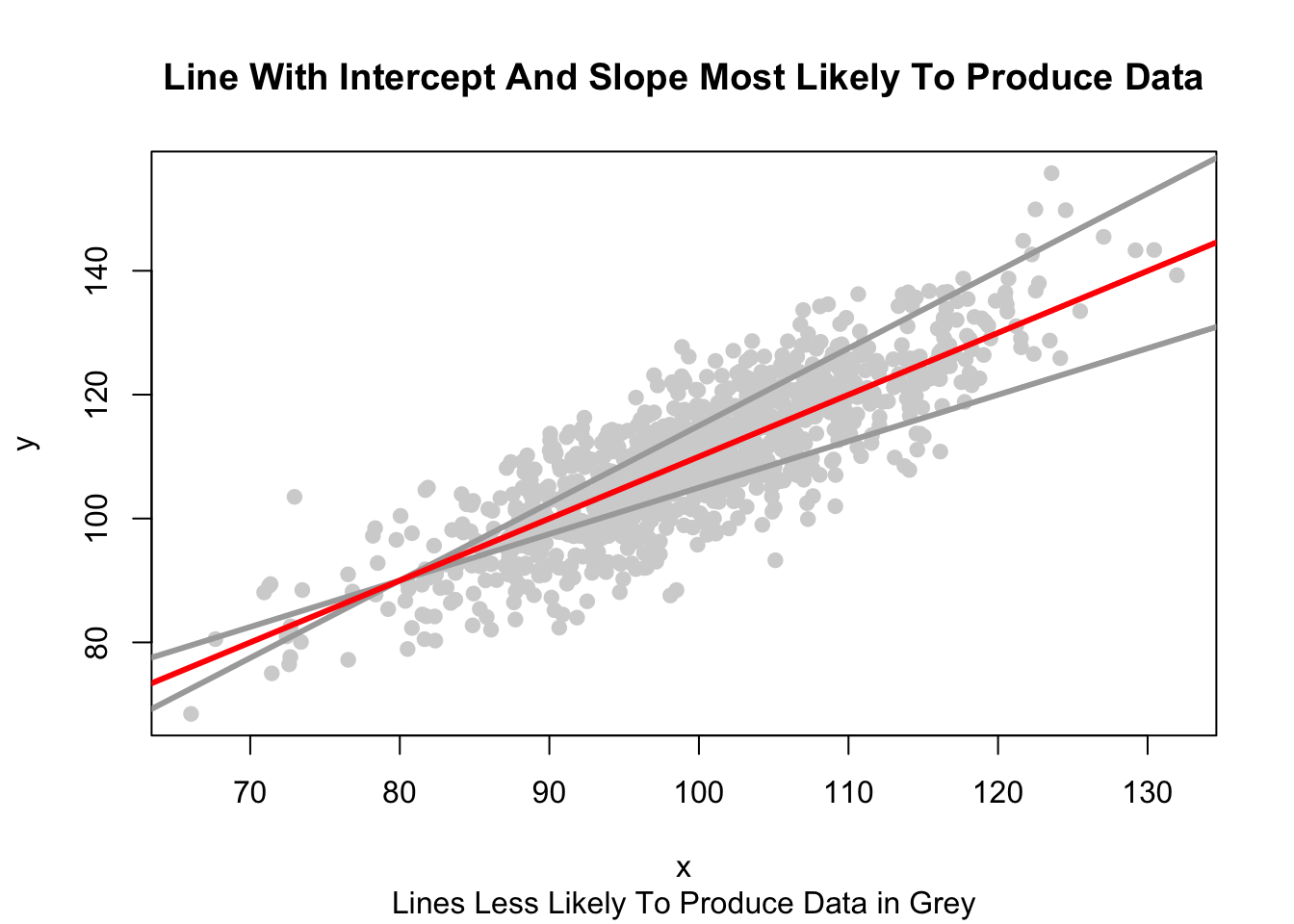
Maximum Likelihood Estimation is essentially the process of finding the combination of parameters (e.g. \(\beta\)) which maximizes the likelihood of producing the data.

Figure 1: Joint Likelihood of Two Parameters

3 An Empirical Example

Figure 2: An Empirical Example

4 Log-Likelihood

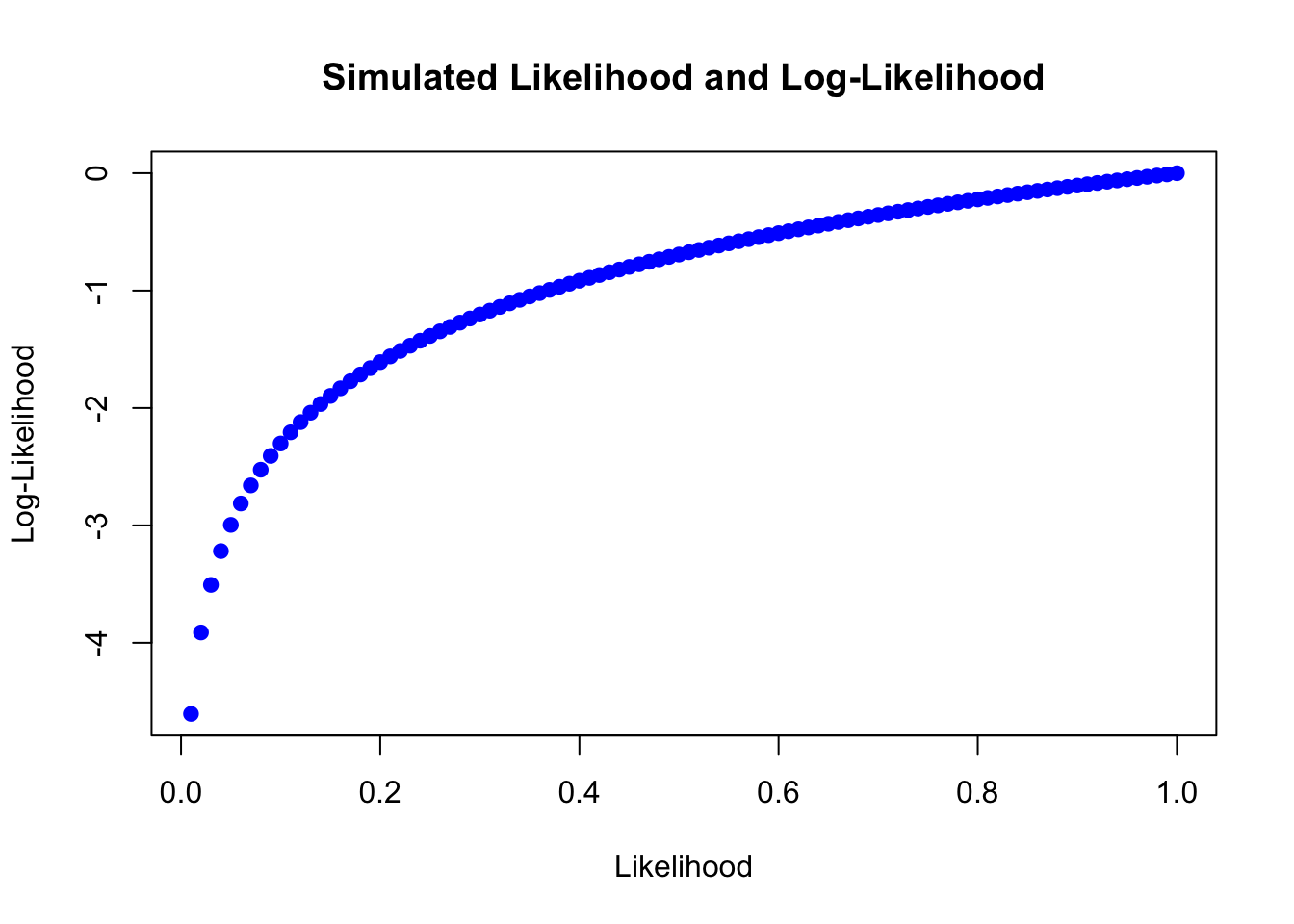
Because probabilities are by definition \(< 1\), the likelihood \(\mathscr{L}\) tends to be a very small number. For a variety of reasons, it is often easier to work with the logarithm of the likelihood: \(\ln \mathscr{L}\).

5 Visualizing the Likelihood and Log-Likelihood

Figure 3: Likelihood and Log-Likelihood

6 Conclusion

Higher values of the log-likelihood, closer to 0, represent models with a better fit.