Show the code
twoway ///
(function y = exp(x)/(1 + exp(x)), range(-10 10) lwidth(thick) lpattern(dash)), ///
title("The Logistic Curve") ///
ytitle("Probablity") ///
scheme(stcolor)
graph export logistic.png, width(2000) replaceThe Logistic Curve Is A Theoretical Construct
1 The Logistic Curve
Equations
The equation for the curve below comes from the logistic regression equation:
\[\ln \Big(\frac{p(\text{outcome})}{1-p(\text{outcome})}\Big) = \beta_0 + \beta_1 x_1\]
We exponentiate both sides of the equation:
\[\frac{p(\text{outcome})}{1-p(\text{outcome})} = e^{\beta_0 + \beta_1 x_1}\]
We multiply both sides by the denominator of the fraction that is on the left hand side of the equation:
\[p(\text{outcome}) = e^{\beta_0 + \beta_1 x_1}(1-p(\text{outcome}))\]
Then:
\[p(\text{outcome}) = e^{\beta_0 + \beta_1 x_1} - e^{\beta_0 + \beta_1 x_1} * p(\text{outcome})\] Then:
\[p(\text{outcome}) + e^{\beta_0 + \beta_1 x_1} * p(\text{outcome}) = e^{\beta_0 + \beta_1 x_1}\]
Then:
\[(1 + e^{\beta_0 + \beta_1 x_1}) * p(\text{outcome}) = e^{\beta_0 + \beta_1 x_1}\]
And, finally:
\[p(\text{outcome}) = \frac{e^{\beta_0 + \beta_1 x_1}}{1 +e^{\beta_0 + \beta_1 x_1}}\]
2 The Logistic Curve is a Theoretical Construct
Key Idea
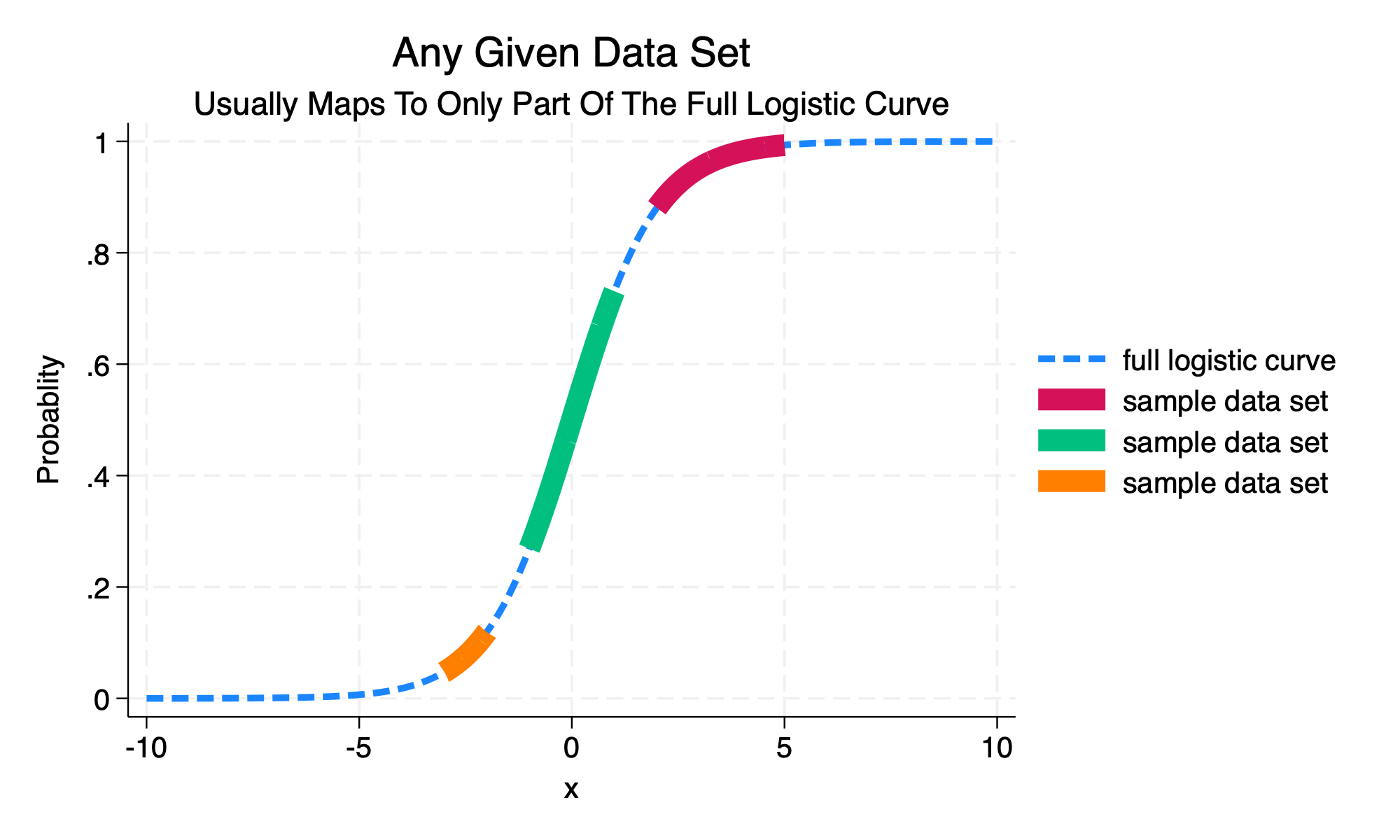
Any given data set usually maps to only part of the full logistic curve.
Show the code
twoway ///
(function y = exp(x)/(1 + exp(x)), range(-10 10) lwidth(thick) lpattern(dash)) /// full logistic curve
(function y = exp(x)/(1 + exp(x)), range(2 5) lwidth(vvthick)) /// sample data set
(function y = exp(x)/(1 + exp(x)), range(-1 1) lwidth(vvthick)) /// sample data set
(function y = exp(x)/(1 + exp(x)), range(-3 -2) lwidth(vvthick) lcolor(orange)), /// sample data set
title("Any Given Data Set") ///
ytitle("Probablity") ///
subtitle("Usually Maps To Only Part Of The Full Logistic Curve") ///
legend(order(1 "full logistic curve" 2 "sample data set" 3 "sample data set" 4 "sample data set") pos(3)) ///
scheme(stcolor)
graph export logistic2.png, width(2000) replace