Simpson’s Paradox

Introduction

Simpson’s Paradox (Simpson, 1951) is the idea that associations between variables that are found between two variables in the sample as a whole, can be very different (or even reversed) when a third variable is introduced.

There are specific mathematical conditions under which Simpson’s Paradox applies. However, thinking through these mathematical conditions may not be helpful to develop intuitions about Simpson’s Paradox.

Careful inspection of visualizations can help us to develop some understanding of Simpson’s Paradox.

The key substantive conclusion is that models of the data that only account for two variables may provide very different–or even opposite–conclusions about a treatment or intervention than models of the data that account for many variables.

Some Hypothetical Data

These data are based on the hypothetical data provided by Simpson (1951).

count	treatment	status	group
4	untreated	alive	A
3	untreated	dead	A
8	treated	alive	A
5	treated	dead	A
2	untreated	alive	B
3	untreated	dead	B
12	treated	alive	B
15	treated	dead	B

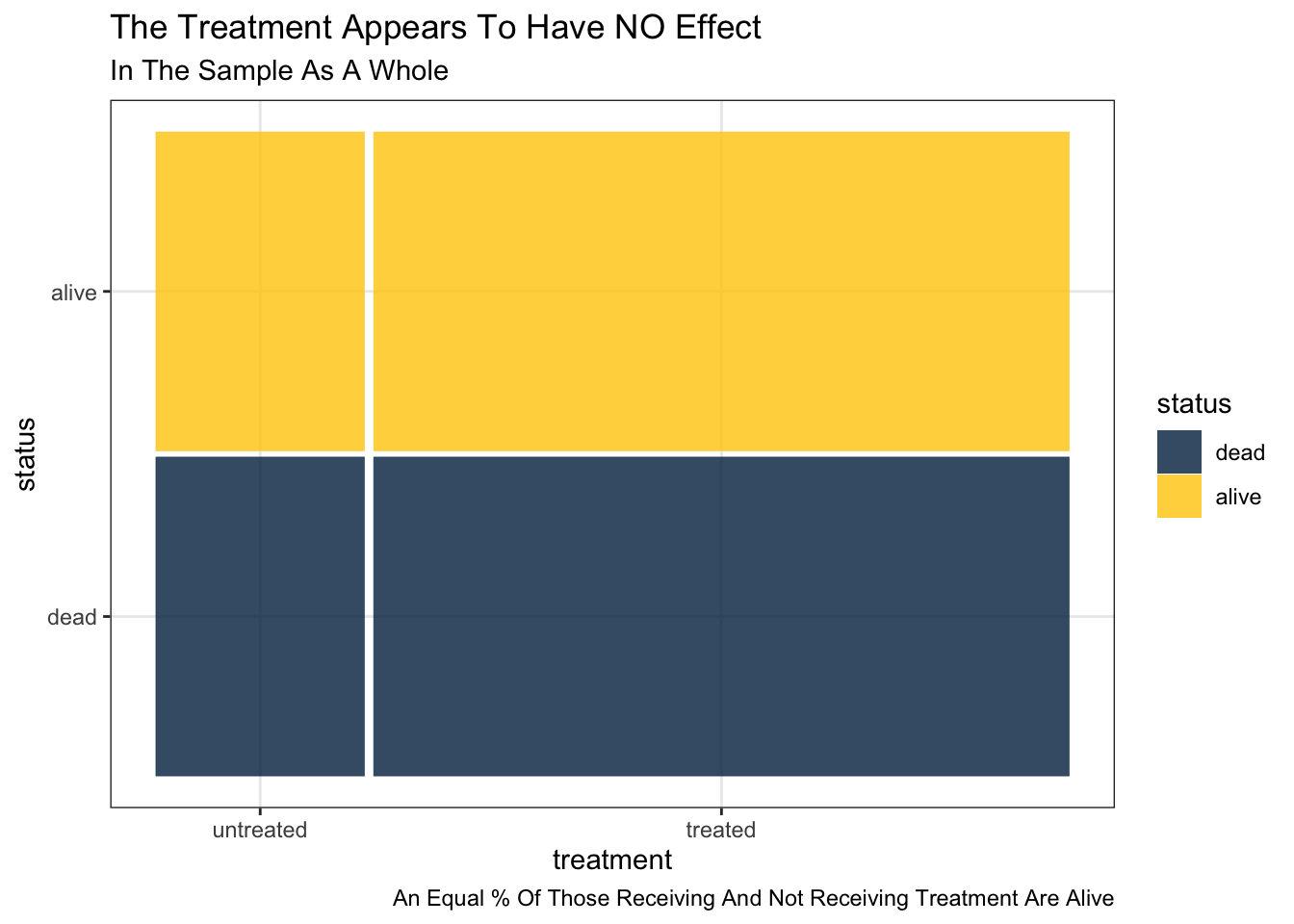
Sample As A Whole

The treatment appears to have NO effect. An equal percentage of those receiving and not receiving treatment are alive.

Cross Tabulation

	dead	alive
untreated	6	6
treated	20	20

Mosaic Plot

Mosaic Plots are a little bit counterintuive at first. However, I believe that–after a little bit of study–Mosaic Plots provide the best visual representation of these relationships.

Pie Chart

A Pie Chart sometimes is more intuitive at first, but actually has less information than a Mosaic Chart.

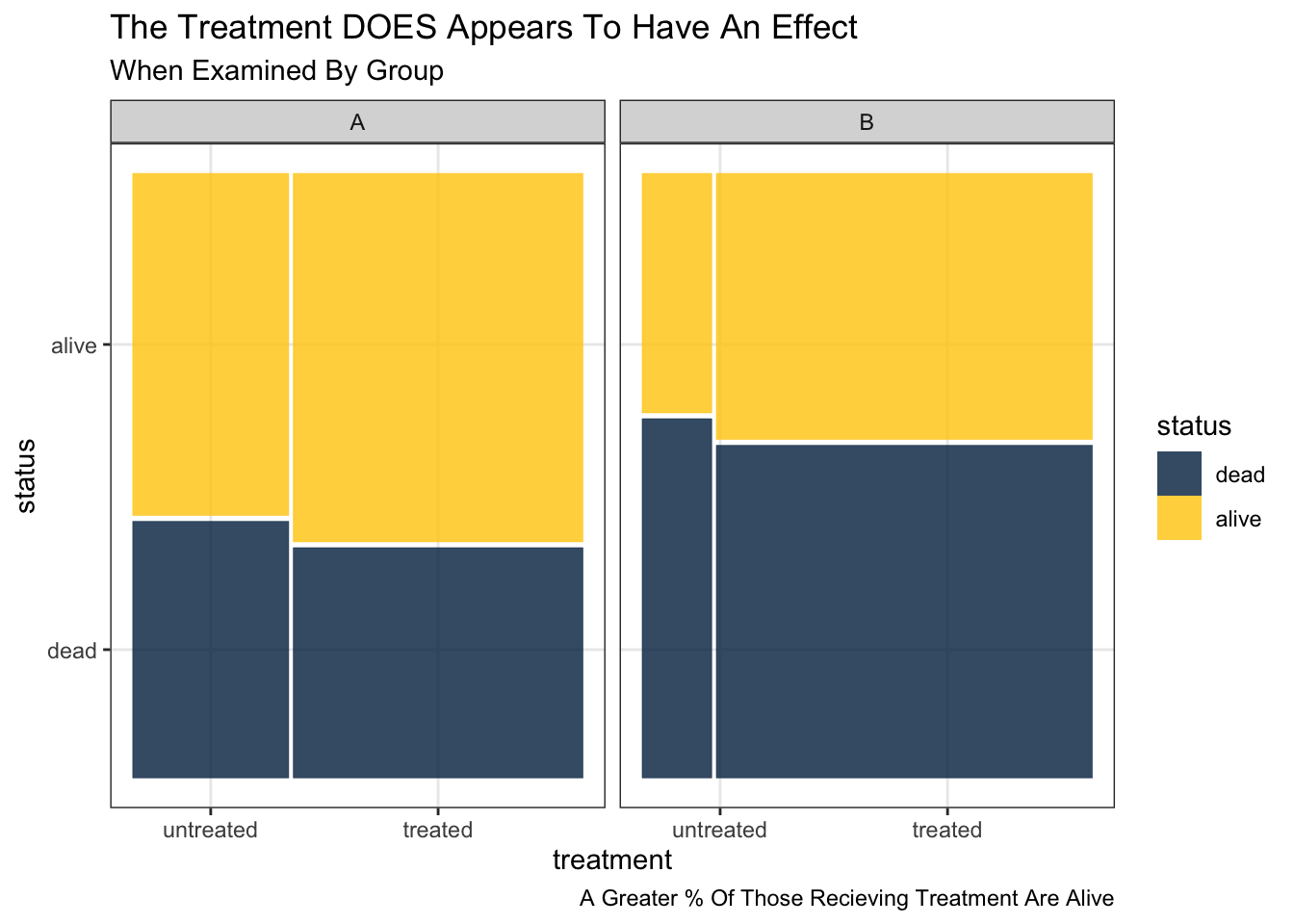
Sample Divided By Groups

The treatment appears to have an effect. A greater percentage of those recieving treatment are alive.

Cross Tabulation

			A	B
untreated	dead		3	3
	alive		4	2
treated	dead		5	15
	alive		8	12

Mosaic Plot

Pie Chart

References

Simpson, E. H. (1951). The interpretation of interaction in contingency tables. Journal of the Royal Statistical Society. Series B (Methodological), 13, 238–241. http://www.jstor.org/stable/2984065