use "simulated_multilevel_data.dta", clear4 Two Level Cross Sectional; And Three Level Longitudinal Models
4.1 Cross Sectional Model
4.1.1 Get Data
4.1.2 The Equation
\[\begin{aligned} \text{outcome}_{ij} = \beta_0 + \beta_1 \text{parental warmth} + \beta_2 \text{physical punishment} + \\ \beta_3 \text{identity} + \beta_4 \text{intervention} + \beta_5 HDI + \\ u_{0j} + u_{1j} \times \text{parental warmth} + e_{ij} \end{aligned} \tag{4.1}\]
4.1.3 Descriptive Statistics
summarize // descriptive statistics Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
country | 3,000 15.5 8.656884 1 30
HDI | 3,000 64.76667 17.24562 33 87
family | 3,000 50.5 28.87088 1 100
id | 0
identity | 3,000 .4976667 .5000779 0 1
-------------+---------------------------------------------------------
intervention | 3,000 .4843333 .4998378 0 1
physical_p~t | 3,000 2.478667 1.360942 0 5
warmth | 3,000 3.521667 1.888399 0 7
outcome | 3,000 52.43327 6.530996 29.60798 74.835534.1.4 Spaghetti Plot
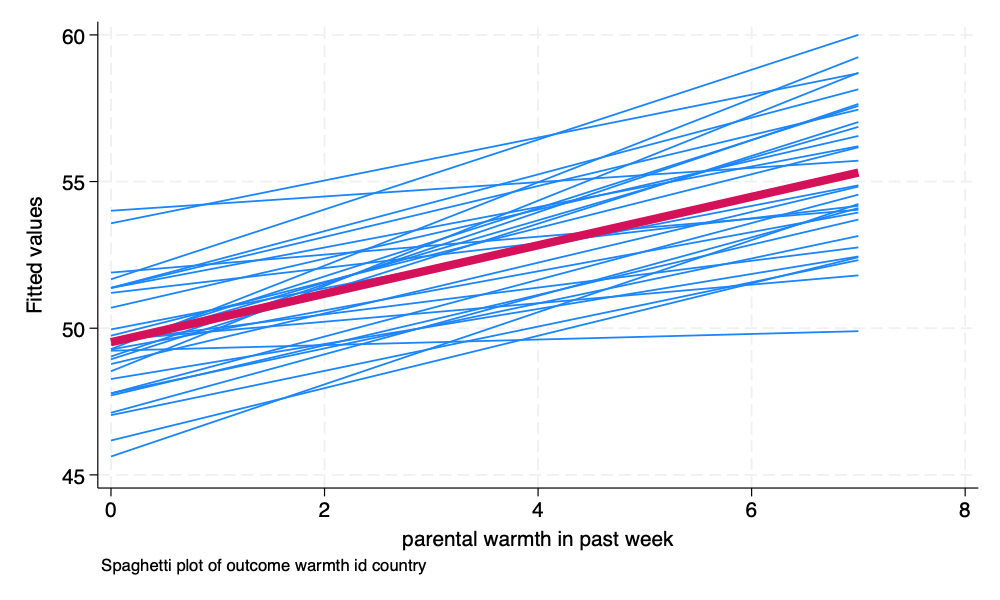
spagplot outcome warmth, id(country) scheme(stcolor)
graph export spagplot1.png, width(1000) replaceThis spaghetti plot is illustrating the idea of random intercepts and random slopes. The multilevel model is estimating group specific regression lines, in this case country specific regression lines. Each country specific regression line has its own intercept and its own slope. The results presented in the multilevel model are the result of averaging these estimates into one overall estimate.
4.1.5 Unconditional Model
4.1.5.1 Model
mixed outcome || country: // unconditional modelPerforming EM optimization ...
Performing gradient-based optimization:
Iteration 0: Log likelihood = -9802.8371
Iteration 1: Log likelihood = -9802.8371
Computing standard errors ...
Mixed-effects ML regression Number of obs = 3,000
Group variable: country Number of groups = 30
Obs per group:
min = 100
avg = 100.0
max = 100
Wald chi2(0) = .
Log likelihood = -9802.8371 Prob > chi2 = .
------------------------------------------------------------------------------
outcome | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
_cons | 52.43327 .3451217 151.93 0.000 51.75685 53.1097
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects parameters | Estimate Std. err. [95% conf. interval]
-----------------------------+------------------------------------------------
country: Identity |
var(_cons) | 3.178658 .9226736 1.799552 5.614658
-----------------------------+------------------------------------------------
var(Residual) | 39.46106 1.024013 37.50421 41.52
------------------------------------------------------------------------------
LR test vs. linear model: chibar2(01) = 166.31 Prob >= chibar2 = 0.00004.1.5.2 ICC
estat iccIntraclass correlation
------------------------------------------------------------------------------
Level | ICC Std. err. [95% conf. interval]
-----------------------------+------------------------------------------------
country | .0745469 .0201254 .0434963 .1248696
------------------------------------------------------------------------------4.1.6 Conditional Model
mixed outcome warmth physical_punishment identity i.intervention HDI || country: warmth // multilevel model
est store crosssectional // store estimatesPerforming EM optimization ...
Performing gradient-based optimization:
Iteration 0: Log likelihood = -9626.6279
Iteration 1: Log likelihood = -9626.607
Iteration 2: Log likelihood = -9626.607
Computing standard errors ...
Mixed-effects ML regression Number of obs = 3,000
Group variable: country Number of groups = 30
Obs per group:
min = 100
avg = 100.0
max = 100
Wald chi2(5) = 334.14
Log likelihood = -9626.607 Prob > chi2 = 0.0000
------------------------------------------------------------------------------------
outcome | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------------+----------------------------------------------------------------
warmth | .8345368 .0637213 13.10 0.000 .7096453 .9594282
physical_punishm~t | -.9916657 .0797906 -12.43 0.000 -1.148052 -.8352791
identity | -.3004767 .2170295 -1.38 0.166 -.7258466 .1248933
1.intervention | .6396427 .2174519 2.94 0.003 .2134448 1.065841
HDI | -.003228 .0199257 -0.16 0.871 -.0422817 .0358256
_cons | 51.99991 1.371257 37.92 0.000 49.3123 54.68753
------------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects parameters | Estimate Std. err. [95% conf. interval]
-----------------------------+------------------------------------------------
country: Independent |
var(warmth) | .0227504 .0257784 .0024689 .2096436
var(_cons) | 2.963975 .9737647 1.556777 5.643163
-----------------------------+------------------------------------------------
var(Residual) | 34.97499 .9097109 33.23668 36.80422
------------------------------------------------------------------------------
LR test vs. linear model: chi2(2) = 205.74 Prob > chi2 = 0.0000
Note: LR test is conservative and provided only for reference.4.2 Longitudinal Model
4.2.1 Get Data
use "simulated_multilevel_longitudinal_data.dta", clear4.2.2 The Equation
\[ \begin{aligned} \text{outcome}_{ij} = \beta_0 + \beta_1 \text{parental warmth} + \beta_2 \text{physical punishment} + \beta_3 \text{time} + \\ \beta_4 \text{identity}_2 + \beta_5 \text{intervention} + \beta_5 HDI + \\ u_{0j} + u_{1j} \times \text{parental warmth} + \\ v_{0i} + v_{1i} \times t + e_{ij} \end{aligned} \tag{4.2}\]
4.2.3 Descriptive Statistics
summarize // descriptive statistics Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
country | 9,000 15.5 8.655922 1 30
HDI | 9,000 64.76667 17.2437 33 87
family | 9,000 50.5 28.86767 1 100
id | 0
identity | 9,000 .4976667 .5000223 0 1
-------------+---------------------------------------------------------
intervention | 9,000 .4843333 .4997823 0 1
t | 9,000 2 .8165419 1 3
physical_p~t | 9,000 2.485333 1.373639 0 5
warmth | 9,000 3.514222 1.8839 0 7
outcome | 9,000 53.37768 6.572285 29.60798 79.021994.2.4 Alternate Plot
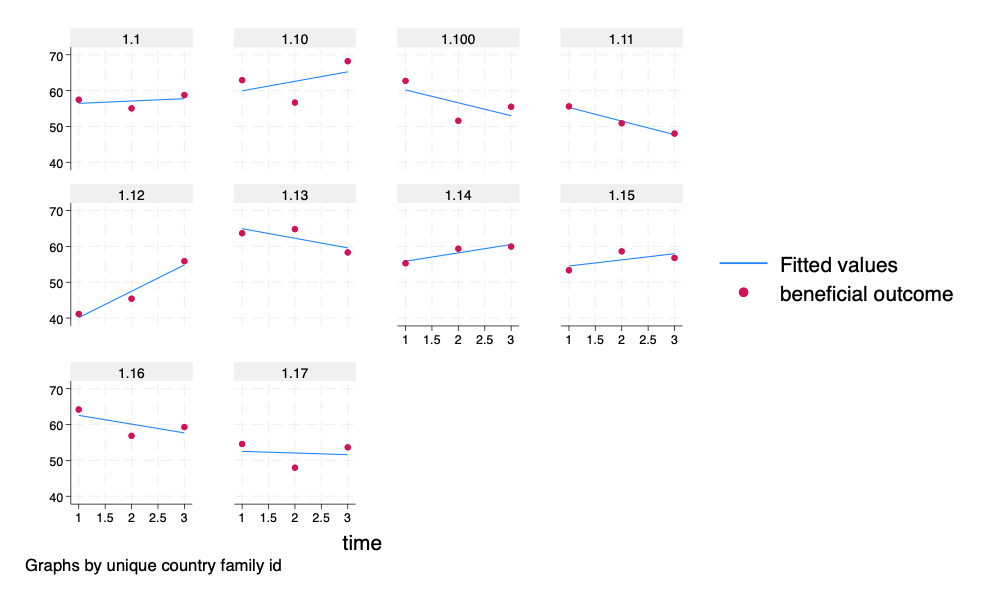
encode id, generate(idNUMERIC) // numeric version of id
* spagplot outcome t if idNUMERIC <= 10, id(idNUMERIC) scheme(stcolor)
twoway (lfit outcome t) (scatter outcome t) if idNUMERIC <= 10, by(idNUMERIC) scheme(stcolor)
graph export spagplot2.png, width(1000) replace4.2.5 Unconditional Model
4.2.5.1 Model
mixed outcome || country: || id: // unconditional model4.2.5.2 ICC
estat iccIntraclass correlation
------------------------------------------------------------------------------
Level | ICC Std. err. [95% conf. interval]
-----------------------------+------------------------------------------------
country | .0748336 .0190847 .0450028 .1219141
id|country | .3462837 .0171461 .3134867 .3806097
------------------------------------------------------------------------------4.2.6 Conditional Model
mixed outcome t warmth physical_punishment i.identity i.intervention HDI || country: warmth || id: t // multilevel model
est store longitudinal // store estimatesPerforming EM optimization ...
Performing gradient-based optimization:
Iteration 0: Log likelihood = -28523.49
Iteration 1: Log likelihood = -28499.953
Iteration 2: Log likelihood = -28499.735
Iteration 3: Log likelihood = -28499.604
Iteration 4: Log likelihood = -28499.603
Computing standard errors ...
Mixed-effects ML regression Number of obs = 9,000
Grouping information
-------------------------------------------------------------
| No. of Observations per group
Group variable | groups Minimum Average Maximum
----------------+--------------------------------------------
country | 30 300 300.0 300
id | 3,000 3 3.0 3
-------------------------------------------------------------
Wald chi2(6) = 1096.15
Log likelihood = -28499.603 Prob > chi2 = 0.0000
------------------------------------------------------------------------------------
outcome | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------------+----------------------------------------------------------------
t | .943864 .0658716 14.33 0.000 .814758 1.07297
warmth | .9134959 .0423732 21.56 0.000 .8304461 .9965458
physical_punishm~t | -1.007897 .0497622 -20.25 0.000 -1.105429 -.9103647
1.identity | -.1276926 .1515835 -0.84 0.400 -.4247908 .1694056
1.intervention | .8589966 .1519094 5.65 0.000 .5612596 1.156734
HDI | -.0005657 .0196437 -0.03 0.977 -.0390666 .0379352
_cons | 50.46724 1.338318 37.71 0.000 47.84418 53.09029
------------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects parameters | Estimate Std. err. [95% conf. interval]
-----------------------------+------------------------------------------------
country: Independent |
var(warmth) | .0107585 .0127845 .0010477 .1104712
var(_cons) | 3.167087 .9146767 1.798155 5.578185
-----------------------------+------------------------------------------------
id: Independent |
var(t) | 5.69e-10 1.29e-07 1.1e-202 3.0e+183
var(_cons) | 8.387268 .4724189 7.510624 9.366236
-----------------------------+------------------------------------------------
var(Residual) | 26.02734 .4753703 25.11211 26.97592
------------------------------------------------------------------------------
LR test vs. linear model: chi2(4) = 1247.03 Prob > chi2 = 0.0000
Note: LR test is conservative and provided only for reference.4.2.7 Nice Table of Results
etable, estimates(crosssectional longitudinal) ///
showstars showstarsnote /// show stars and note
column(estimate) // column is modelname crosssectional longitudinal
----------------------------------------------------------------
parental warmth in past week 0.835 ** 0.913 **
(0.064) (0.042)
physical punishment in past week -0.992 ** -1.008 **
(0.080) (0.050)
hypothetical identity group variable -0.300
(0.217)
recieved intervention
1 0.640 ** 0.859 **
(0.217) (0.152)
Human Development Index -0.003 -0.001
(0.020) (0.020)
time 0.944 **
(0.066)
hypothetical identity group variable
1 -0.128
(0.152)
Intercept 52.000 ** 50.467 **
(1.371) (1.338)
var(warmth) 0.023 0.011
(0.026) (0.013)
var(_cons) 2.964 3.167
(0.974) (0.915)
var(e) 34.975 26.027
(0.910) (0.475)
var(_cons) 8.387
(0.472)
var(t) 0.000
(0.000)
Number of observations 3000 9000
----------------------------------------------------------------
** p<.01, * p<.05