2 Estimation of p Values
2.1 Grouped and Individual Data
Bland and Altman (1994) suggested the following procedure for simulating some data:
“The data were generated from random numbers, and there is no relation between X and Y at all. Firstly, values of X and Y were generated for each ‘subject,’ then a further random number was added to make the individual observation.” (Bland and Altman 1994)
So… we follow their procedure.
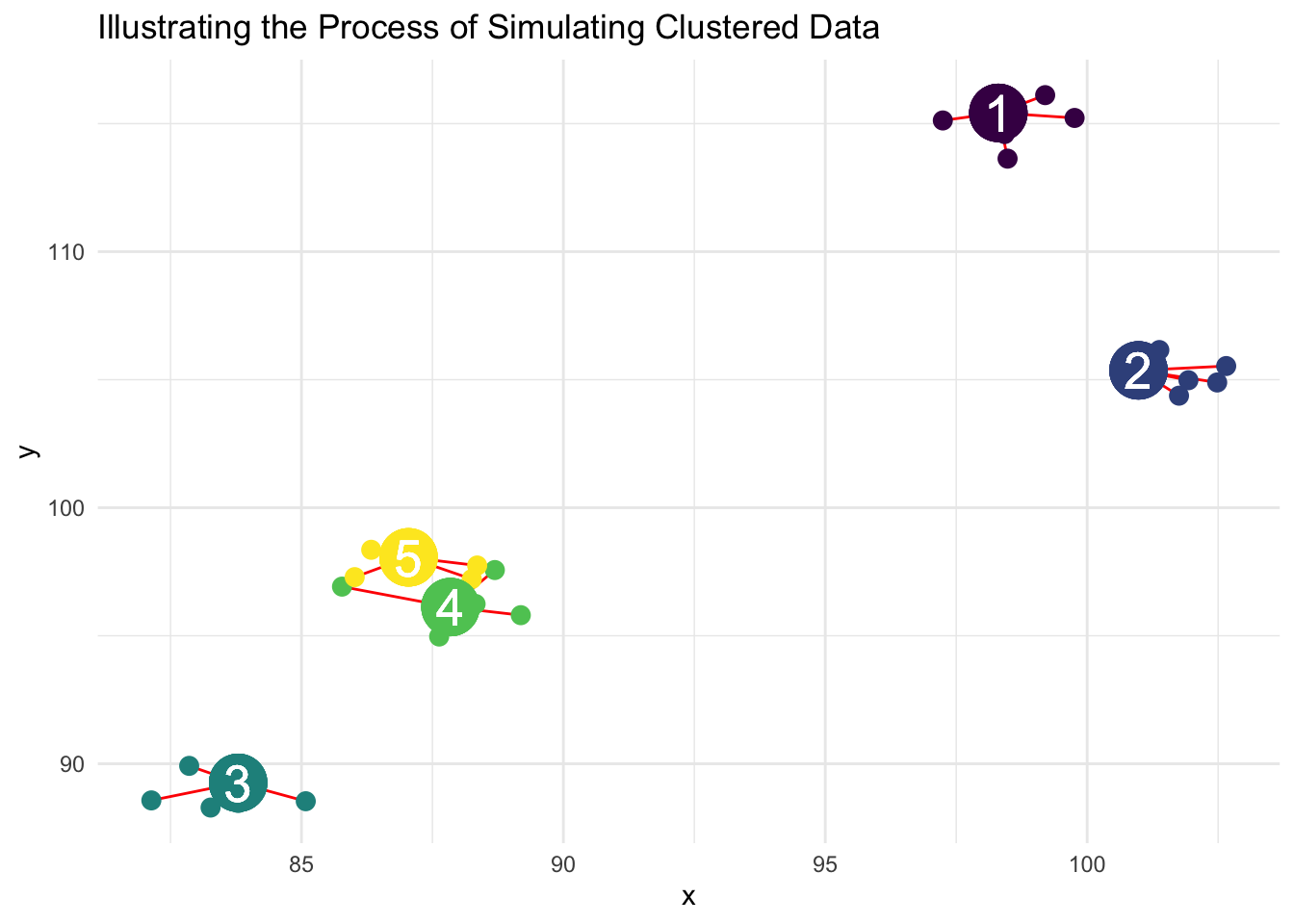
Simulating The Data
The graph below illustrates the process of simulating the data.
2.2 Analyses
2.2.1 OLS
An OLS analysis indicates that there is a statistically significant association of \(x\) and \(y\).
OLS1
-------------------------------
x_individual 1.046 **
Intercept 4.488
Number of observations 25
-------------------------------
** p<.01, * p<.052.2.2 MLM
In contrast, an MLM analysis (correctly) finds that there is no statistically significant association of \(x\) and \(y\).
MLM1
--------------------------------
x_individual 0.039
Intercept 97.005 **
var(_cons) 74.523
var(e) 0.594
Number of observations 25
--------------------------------
** p<.01, * p<.052.2.3 Compare OLS and MLM
OLS1 MLM1
-----------------------------------------
x_individual 1.046 ** 0.039
Intercept 4.488 97.005 **
var(_cons) 74.523
var(e) 0.594
Number of observations 25 25
-----------------------------------------
** p<.01, * p<.05