3 Estimation of \(\beta\) Coefficients
3.1 Introduction
Associations between two variables can be very different (or even reversed) depending upon whether or not the analysis is “aware” of the grouped, nested, or clustered nature of the data (Nieuwenhuis 2015; Diez Roux 2003; Gelman et al. 2007). In multilevel analysis, the groups are often schools, neighborhoods, communities, or countries.
A model that is “aware” of the clustered nature of the data may provide very different–likely better–substantive conclusions than a model that is not aware of the clustered nature of the data. This phenomena is closely related to the “ecological fallacy”: the idea that group level and individual level relationships are not necessarily the same (Firebaugh 2001).
3.2 Graphs
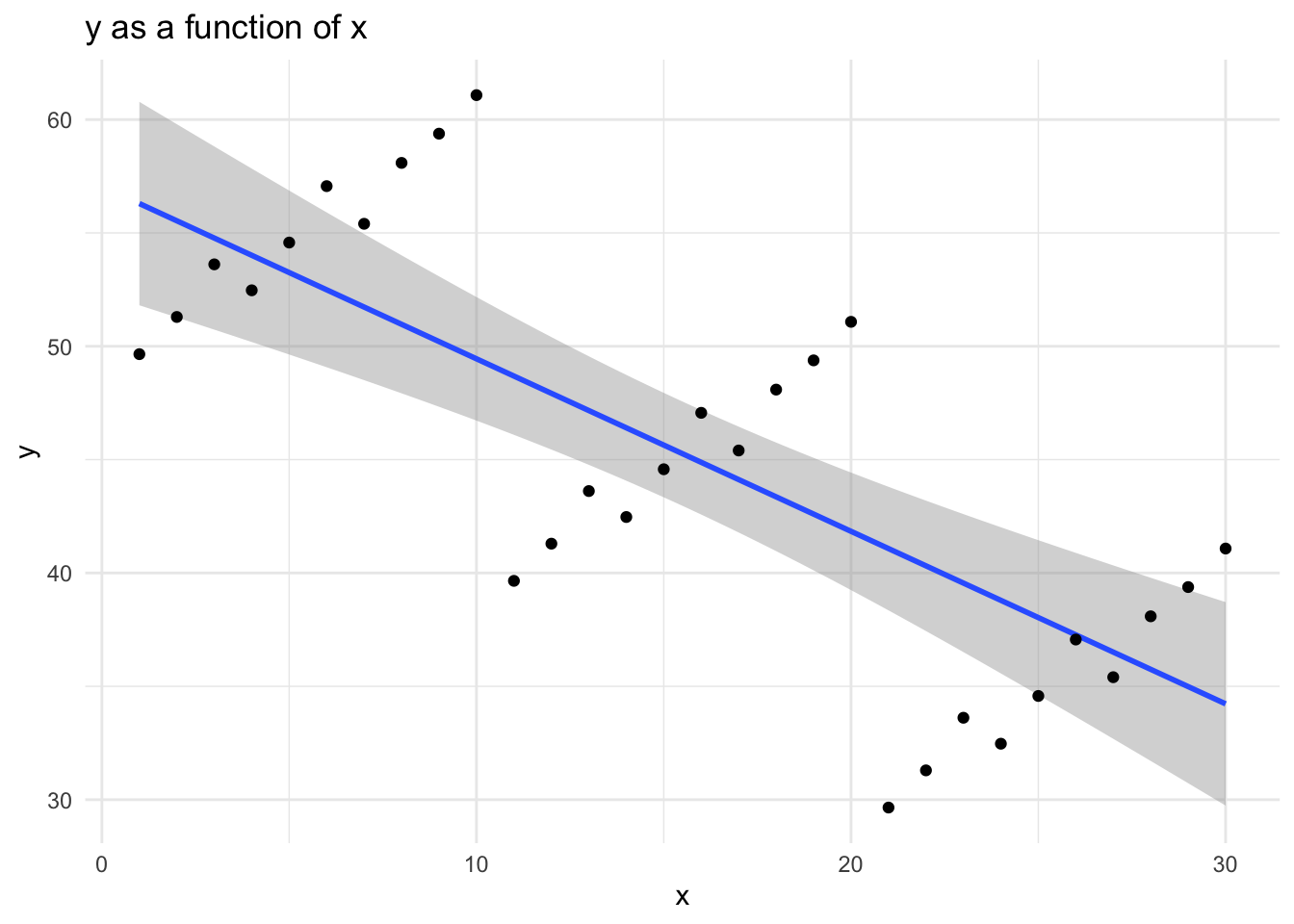
3.2.1 A “Naive” Graph
This “naive” graph is unaware of the grouped nature of the data.
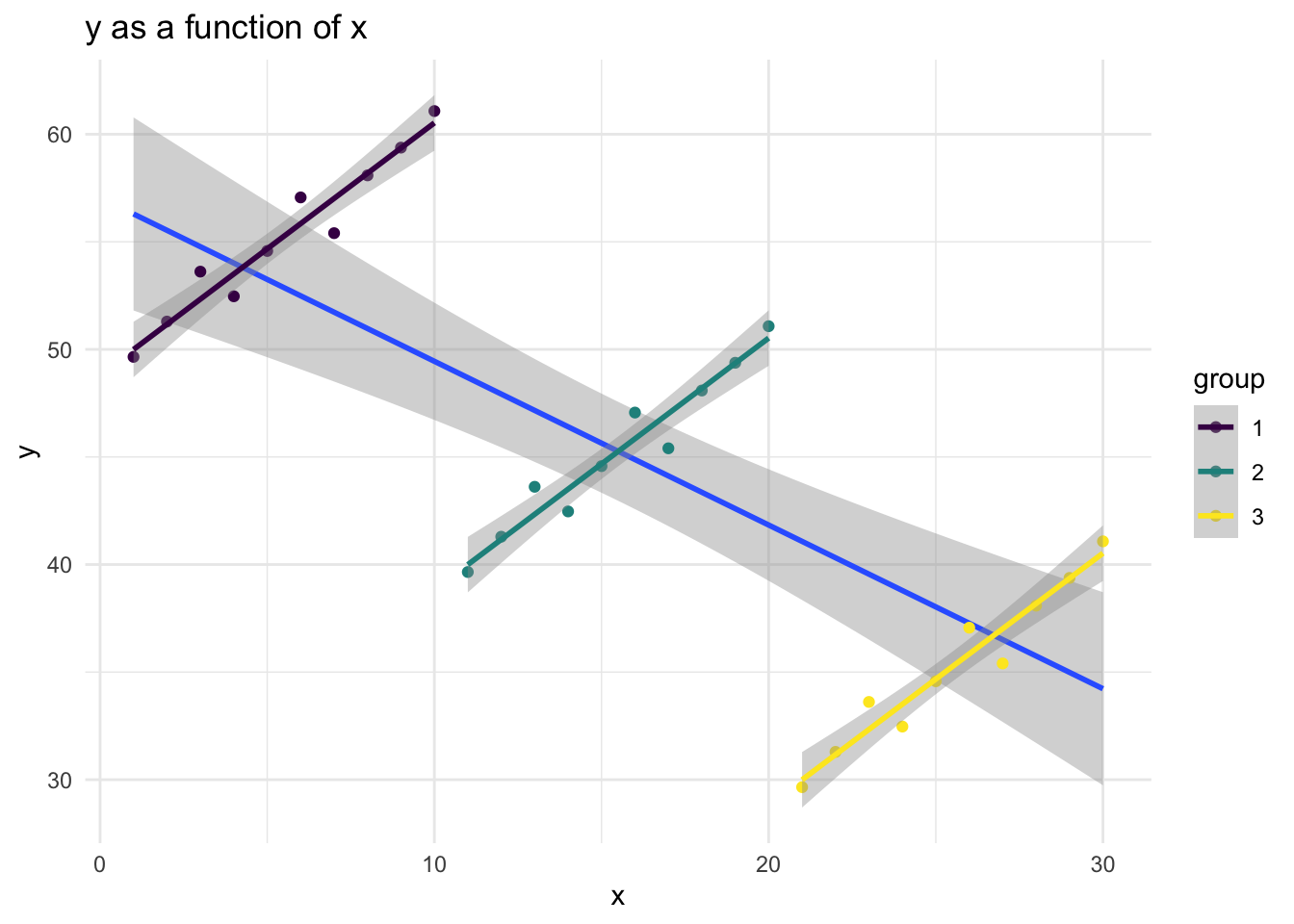
3.2.2 An “Aware” Graph
This “aware” graph is aware of the grouped nature of the data.
3.3 Regressions
3.3.1 A “Naive” OLS Analysis
The OLS model with only x as a covariate is not aware of the grouped structure of the data, and the coefficient for x reflects this.
OLS2
--------------------------------
x -0.761 **
Intercept 57.057 **
Number of observations 30
--------------------------------
** p<.01, * p<.053.3.2 An “Aware” MLM Analysis
The multilevel model is aware of the grouped structure of the data, and the coefficient for x reflects this.
MLM2
---------------------------------
x 1.166 **
Intercept 27.192 **
var(_cons) 312.623
var(e) 0.806
Number of observations 30
---------------------------------
** p<.01, * p<.053.3.3 Compare The Models
OLS2 MLM2
-------------------------------------------
x -0.761 ** 1.166 **
Intercept 57.057 ** 27.192 **
var(_cons) 312.623
var(e) 0.806
Number of observations 30 30
-------------------------------------------
** p<.01, * p<.053.4 A Thought Experiment
When might a situation like this arise in practice? This is surprisingly difficult to think through.
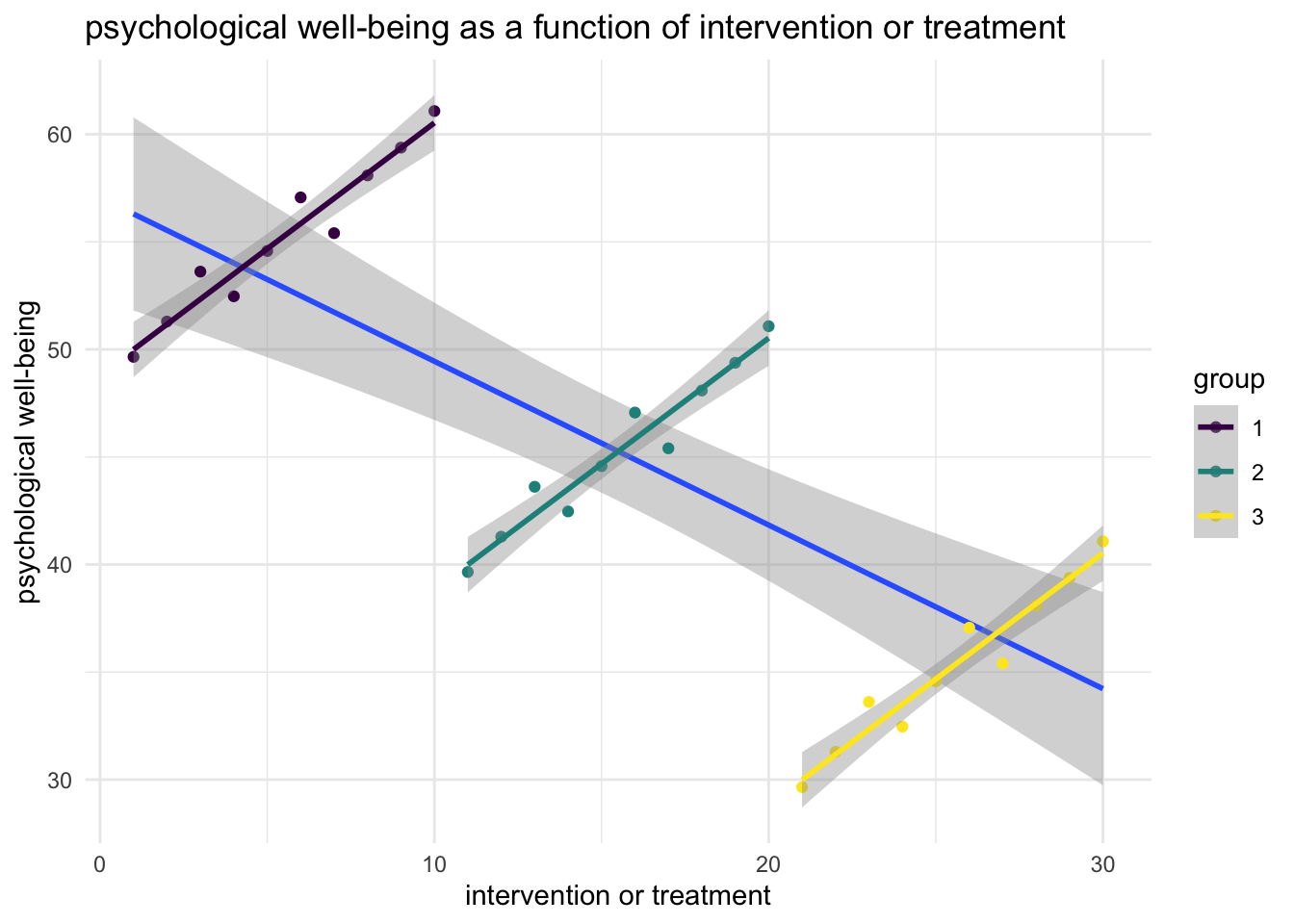
Imagine that x is a protective factor, or an intervention or treatment. Imagine that y is a desirable outcome, like improved mental health or psychological well being.
Now imagine that people provide more of the protective factor or more of the intervention in communities where there are lower levels of the desirable outcome. If we think about it, this is a very plausible situation.
A naive analysis that was unaware of the grouped nature of the data would therefore misconstrue the results, suggesting that the intervention was harmful, when it was in fact helpful.
These data are constructed to provide this kind of extreme example, but it easy to see how multilevel analysis may provide better answers than we would get if we ignored the grouped nature of the data.